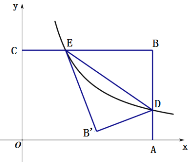
【题目】如图,平面直角坐标系xOy中,线段BC∥x轴、线段AB∥y轴,点B坐标为(4,3),反比例函数y=![]() (x>0)的图像与线段AB交于点D,与线段BC交于点E,连结DE,将△BDE沿DE翻折至△B'DE处,则点B'的纵坐标是( )
(x>0)的图像与线段AB交于点D,与线段BC交于点E,连结DE,将△BDE沿DE翻折至△B'DE处,则点B'的纵坐标是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
参考答案:
【答案】B
【解析】
先根据矩形的性质和点B坐标把D、E的坐标计算出来,再计算BE、BD、ED的长度,利用对称和等面积法把BF的长度计算出来,最后根据勾股定理计算即可得到答案;
解:∵四边形OABC是矩形,
∴CB∥x轴,AB∥y轴,
∵点B坐标为(4,3),
∴D的横坐标为4,E的纵坐标为3,
∵D、E在反比例函数y=![]() (x>0)的图像上,
(x>0)的图像上,
∴D的坐标为:(4,1),E的坐标为:(![]() ,3),
,3),
∴BE=4-![]() =
= ![]() , BD=3-1=2,
, BD=3-1=2,
∴![]() ,
,
连接BB′,交ED于F,过B′作B′G⊥BC于G,如图:
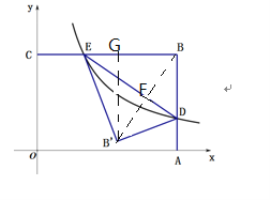
∵B,B′关于ED对称,
∴BF=B′F,BB′⊥ED,
∴BFED=BEBD,
即:![]() ,
,
∴![]() ,
,
∴BB′=![]() ,
,
设EG=x,则BG=![]() -x,
-x,
![]() ,
,
∴![]() ,
,
解得:![]() ,
,
∴EG![]() ,
,
∴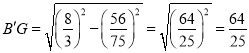 ,
,
则点B'的纵坐标为:![]() ,
,
故选B.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,Rt△ABC中,∠ABC=90°,点D,F分别是AC,AB的中点,CE∥DB,BE∥DC.
(1)求证:四边形DBEC是菱形;
(2)若AD=3,DF=1,求四边形DBEC面积.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,在平面直角坐标系中,O是坐标原点,矩形OACB的顶点A、B分别在
 轴和
轴和 轴上,已知OA=5,OB=3,点D的坐标是(0,1),点P从点B出发以每秒1个单位的速度沿折线BCA的方向运动,当点P与点A重合时,运动停止,设运动的时间为
轴上,已知OA=5,OB=3,点D的坐标是(0,1),点P从点B出发以每秒1个单位的速度沿折线BCA的方向运动,当点P与点A重合时,运动停止,设运动的时间为 秒.
秒.
(1)点P运动到与点C重合时,求直线DP的函数解析式;
(2)求△OPD的面积S关于
 的函数解析式,并写出对应
的函数解析式,并写出对应 的取值范围;
的取值范围;(3)点P在运动过程中,是否存在某些位置使△ADP是不以DP为底边的等腰三角形,若存在,请求出点P的坐标;若不存在,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在等腰Rt△ABC中,∠ACB=90°,AC=BC=8,点D在△ABC外,连接AD、BD,且∠ADB=90°,AB、CD相交于点E,AB、CD的中点分别是点F、G,连接FG.

(1)求AB的长;
(2)求证:AD+BD=
 CD;
CD;(3)若BD=6,求FG的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,二次函数的图象与x轴相交于A(﹣3,0)、B(1,0)两点,与y轴相交于点C(0,3),点C、D是二次函数图象上的一对对称点,一次函数的图象过点B、D.

(1)求D点坐标;
(2)求二次函数的解析式;
(3)根据图象直接写出使一次函数值小于二次函数值的x的取值范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在⊙O中,直径AB=6,BC是弦,∠ABC=30°,点P在BC上,点Q在⊙O上,且OP⊥PQ.
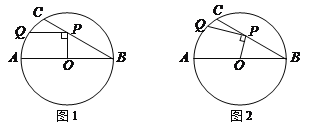
(1)如图1,当PQ∥AB时,求PQ的长度;
(2)如图2,当点P在BC上移动时,求PQ长的最大值.
相关试题

