【题目】如图,抛物线y=﹣x2+bx+c经过A(﹣1,0),C(0,4)两点,与x轴交于另一点B,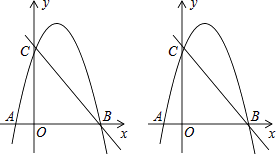
(1)求抛物线的解析式;
(2)求P在第一象限的抛物线上,P点的横坐标为t,过点P向x轴做垂线交直线BC于点Q,设线段PQ的长为m,求m与t之间的函数关系式并求出m的最大值;
(3)在(2)的条件下,抛物线上一点D的纵坐标为m的最大值,连接BD,在抛物线是否存在点E(不与点A,B,C重合)使得∠DBE=45°?若不存在.请说明理由;若存在请求E点的坐标.
参考答案:
【答案】
(1)
解:抛物线y=﹣x2+bx+c经过A(﹣1,0)、C(0,4)两点,
∴ ![]() 解得
解得 ![]()
∴抛物线的解析式y=﹣x2+3x+4
(2)
解:令﹣x2+3x+4=0,
解得x1=﹣1,x2=4,
∴B(4,0)
设直线BC的解析式为y=kx+a
∴ ![]() 解得
解得 ![]() ,
,
∴直线BC的解析式为y=﹣x+4
设P点的坐标为(t,﹣t2+3t+4),则Q点的坐标为(t,﹣t+4)
∴m=(﹣t2+3t+4)﹣(﹣t+4)=﹣(t﹣2)2+4
整理得m=﹣(t﹣2)2+4,
∴当t=2时,m的最大值为4
(3)
解:存在
∵抛物线一点D的纵坐标为m的最大值4,
∴﹣x2+3x+4=4,解得x1=0(舍),x2=3
∴D(3,4),CD=3
∵C(0,4),
∴CD∥x轴,
∵OC=OB=4,
∴△BOC为直角三角形,
过点D作DH⊥BC于H,过点E作EF⊥x于点F,在△CDB中,CD=3,∠DCB=45°
∴CH=DH= ![]() ,
,
∵CB=4 ![]() ,∴BH=CB﹣CH=
,∴BH=CB﹣CH= ![]()
∵∠DBE=∠CBO=45°
∴∠DBE﹣∠CBE=∠CBO﹣∠CBE,
即∠DBC=∠EBF
∴tan∠DBC= ![]() =
= ![]() =
= ![]()
设EF=3a∴BF=5a
∴OF=5a﹣4
∴F(4﹣5a,0),E(4﹣5a,3a)
∵点E在抛物线上
∴3a=﹣(4﹣5a)2+3(4﹣5a)+4
解得a1=0 a2= ![]()
∴E(﹣ ![]() ,
, ![]() ).
).

【解析】(1)把点A、B的坐标代入抛物线解析式,解关于b、c的方程组求出b、c的值即可得到抛物线解析式,令y=0,解关于x的一元二次方程即可得到点C的坐标;(2)根据抛物线的解析式y=﹣x2+3x+4,令y=0求得点B的坐标为(4.0),设直线BC的解析式为y=kx+a把点B、C的坐标代入直线BC的解析式为y=kx+a,解关于k、a的方程组求出k、a的值,所以直线BC的解析式为y=﹣x+4,设P点的坐标为(t,﹣t2+3t+4),则Q点的坐标为(t,﹣t+4),所以m=(﹣t2+3t+4)﹣(﹣t+4),整理得m=﹣(t﹣2)2+4,根据关于m、t的二次函数即可求得.(3)根据m的最大值是4,代入y=﹣x2+3x+4,可求得D点的坐标(3,4),过D点作DH⊥BC,过E点作EF⊥x轴,由OC=OB=4得△DCB为等腰直角三角形,从而得出△CDH为等腰直角三角形,通过等腰直角三角形求得CN、BH的值,然后根据三角形相似求得EF、BF的关系,设出E点的坐标,然后代入y=﹣x2+3x+4即可求得.
【考点精析】本题主要考查了二次函数的性质的相关知识点,需要掌握增减性:当a>0时,对称轴左边,y随x增大而减小;对称轴右边,y随x增大而增大;当a<0时,对称轴左边,y随x增大而增大;对称轴右边,y随x增大而减小才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如果关于
 的分式方程
的分式方程 有负分数解,且关于
有负分数解,且关于 的不等式组
的不等式组 的解集为
的解集为 ,那么符合条件的所有整数
,那么符合条件的所有整数 的积是( )
的积是( )A.
 B. 0 C. 3 D. 9
B. 0 C. 3 D. 9 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点
 是反比例函数
是反比例函数 图像上一点,作
图像上一点,作 轴于点
轴于点 ,且
,且 的面积为
的面积为 ,点
,点 坐标为
坐标为 .
.
(
 )求
)求 和
和 的值.
的值.(
 )若直线
)若直线 经过点
经过点 ,交另一支双曲线于点
,交另一支双曲线于点 ,求
,求 的面积.
的面积.(
 )指出
)指出 取何值时,一次函数的值大于反比例函数的值,直接写出结果.
取何值时,一次函数的值大于反比例函数的值,直接写出结果. -
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC中,∠ACB是锐角,点D在射线BC上运动,连接AD,将线段AD绕点A逆时针旋转90°,得到AE,连接EC.
(1)操作发现:
若AB=AC,∠BAC=90°,当D在线段BC上时(不与点B重合),如图①所示,请你直接写出线段CE和BD的位置关系和数量关系是 , ;
(2)猜想论证:
在(1)的条件下,当D在线段BC的延长线上时,如图②所示,请你判断(1)中结论是否成立,并证明你的判断.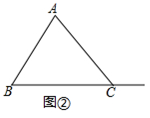
(3)拓展延伸:
如图③,若AB≠AC,∠BAC≠90°,点D在线段BC上运动,试探究:当锐角∠ACB等于度时,线段CE和BD之间的位置关系仍成立(点C、E重合除外)?此时若作DF⊥AD交线段CE于点F,且当AC=3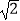 时,请直接写出线段CF的长的最大值是
时,请直接写出线段CF的长的最大值是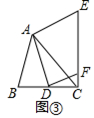
-
科目: 来源: 题型:
查看答案和解析>>【题目】观察下列各式:
13+23=1+8=9,而(1+2)2=9,∴13+23=(1+2)2;
13+23+33=36,而(1+2+3)2=36,∴13+23+33=(1+2+3)2;
13+23+33+43=100,而(1+2+3+4)2=100,∴13+23+33+43=(1+2+3+4)2;
∴13+23+33+43+53=(______ )2= ______ .
根据以上规律填空:
(1)13+23+33+…+n3=(______ )2=[ ______ ]2.
(2)猜想:113+123+133+143+153= ______ .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,Rt△OAB的顶点A在x轴的正半轴上,顶点B的坐标为(3,
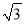 ),点C的坐标为(
),点C的坐标为( ,0),点P为斜边OB上的一个动点,则PA+PC的最小值为( )
,0),点P为斜边OB上的一个动点,则PA+PC的最小值为( )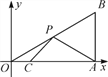
A.
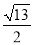 B.
B. 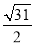 C.
C. 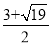 D. 2
D. 2 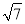
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在ABCD中,AB=6,AD=9,∠BAD的平分线交BC于点E,交DC的延长线于点F,BG⊥AE,垂足为G,BG=
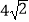 ,则△CEF的周长为( )
,则△CEF的周长为( ) 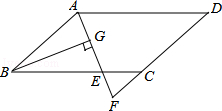
A.8
B.9.5
C.10
D.11.5
相关试题

