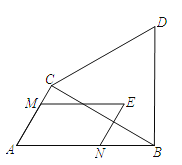
【题目】如图,在Rt△ABC中,∠ACB=90°,∠A=60°,AB=6,△BCD为等边三角形,点E为△BCD围成的区域(包括各边)内的一点,过点E作EM∥AB,交直线AC于点M,作EN∥AC,交直线AB于点N,则![]() 的最大值为_____.
的最大值为_____.
参考答案:
【答案】![]()
【解析】
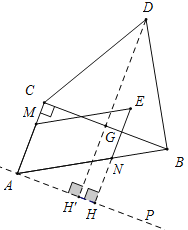
作辅助线,构建30度的直角三角形将![]() 转化为NH,将,即:过A点作AM∥BC,过
转化为NH,将,即:过A点作AM∥BC,过![]() 作
作![]() 交
交![]() 的延长线于点
的延长线于点![]() ,
,![]() ,由△BCD围成的区域(包括各边)内的一点到直线AP的最大值时E在D点时,通过直角三角形性质和勾股定理求出DH’即可得到结论.
,由△BCD围成的区域(包括各边)内的一点到直线AP的最大值时E在D点时,通过直角三角形性质和勾股定理求出DH’即可得到结论.
解:过A点作AP∥BC,过![]() 作
作![]() 交
交![]() 的延长线于点
的延长线于点![]() ,
,
![]() ,
,![]() ,
,
![]() 四边形
四边形![]() 是平行四边形,
是平行四边形,
设![]() ,
,![]() ,
,
∵∠ACB=90°,∠CAB=60°,
∴∠CAM=90°,∠NAH=30°,
![]() 中,
中,![]() ,
,
∵NE∥AC,NH∥AC,
∴E、N、H在同一直线上,
![]()
![]() ,
,
由图可知:△BCD围成的区域(包括各边)内的一点到直线AM距离最大的点在D点,
过D点作![]() ,垂足为
,垂足为![]() .
.
当![]() 在点
在点![]() 时,
时,![]() =
=![]() 取最大值.
取最大值.
∵∠ACB=90°,∠A=60°,AB=6,,
∴AC=3,AB=![]() ,四边形ACGH’是矩形,
,四边形ACGH’是矩形,
∴![]() ,
,
∵△BCD为等边三角形,![]() ,
,
∴![]() =
=![]() ,
,
∴![]() ,
,
∴![]() 的最大值为
的最大值为![]() ,
,
故答案为:![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知AOBC的顶点O(0,0),A(﹣1,2),点B在x轴正半轴上按以下步骤作图:①以点O为圆心,适当长度为半径作弧,分别交边OA,OB于点D,E;②分别以点D,E为圆心,大于
 DE的长为半径作弧,两弧在∠AOB内交于点F;③作射线OF,交边AC于点G,则点G的坐标为( )
DE的长为半径作弧,两弧在∠AOB内交于点F;③作射线OF,交边AC于点G,则点G的坐标为( )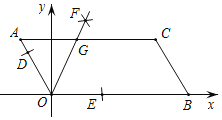
A. (
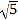 ﹣1,2) B. (
﹣1,2) B. (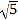 ,2) C. (3﹣
,2) C. (3﹣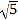 ,2) D. (
,2) D. (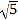 ﹣2,2)
﹣2,2) -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,湛河两岸AB与EF平行,小亮同学假期在湛河边A点处,测得对岸河边C处视线与湛河岸的夹角∠CAB=37°,沿河岸前行140米到点B处,测得对岸C处的视线与湛河岸夹角∠CBA=45°.问湛河的宽度约多少米?(参考数据:sin37°≈0.60,cos37°=0.80,tan37°=0.75)

-
科目: 来源: 题型:
查看答案和解析>>【题目】在《科学》课上,老师讲到温度计的使用方法及液体的沸点时,好奇的王红同学准备测量食用油的沸点,已知食用油的沸点温度高于水的沸点温度(
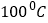 ),王红家只有刻度不超过
),王红家只有刻度不超过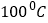 的温度计,她的方法是在锅中倒入一些食用油,用煤气灶均匀加热,并每隔
的温度计,她的方法是在锅中倒入一些食用油,用煤气灶均匀加热,并每隔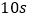 测量一次锅中油温,测量得到的数据如下表:
测量一次锅中油温,测量得到的数据如下表:时间
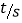
0
10
20
30
40
油温
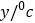
10
30
50
70
90
王红发现,烧了
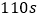 时,油沸腾了,则下列说法不正确的是( )
时,油沸腾了,则下列说法不正确的是( )A. 没有加热时,油的温度是
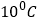
B. 加热
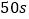 ,油的温度是
,油的温度是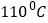
C. 估计这种食用油的沸点温度约是
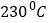
D. 每加热
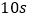 ,油的温度升高
,油的温度升高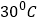
-
科目: 来源: 题型:
查看答案和解析>>【题目】某车行经销的
 型自行车去年
型自行车去年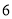 月份销售总额为
月份销售总额为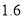 万元,今年由于改造升级每辆车售价比去年增加
万元,今年由于改造升级每辆车售价比去年增加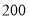 元,今年
元,今年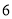 月份与去年同期相比,销售数量相同,销售总额增加
月份与去年同期相比,销售数量相同,销售总额增加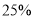 .
.(1)求今年
 型车每辆售价多少元?
型车每辆售价多少元?(2)该车行计划
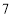 月份用不超过
月份用不超过 万元的资金新进一批
万元的资金新进一批 型车和
型车和 型车共
型车共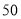 辆,应如何进货才能使这批车售完后获利最多?
辆,应如何进货才能使这批车售完后获利最多?今年
 、
、 两种型号车的进价和售价如下表:
两种型号车的进价和售价如下表: 型车
型车 型车
型车进价(元/辆)
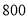
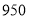
售价(元/辆)
今年售价
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知AB∥CD,若按图中规律继续下去,则∠1+∠2+…+∠n等于( )


A. n·180° B. 2n·180° C. (n-1)·180° D. (n-1)2·180°
-
科目: 来源: 题型:
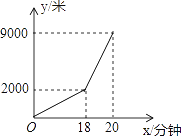
查看答案和解析>>【题目】小亮早晨从家骑车到学校,先上坡后下坡,所行路程y(米)与时间x(分钟)的关系如图所示,若返回时上坡、下坡的速度仍与去时上、下坡的速度分别相同,则小明从学校骑车回家用的时间是________分钟.
相关试题

