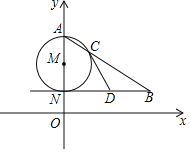
【题目】如图,AN是⊙M的直径,NB∥x轴,AB交⊙M于点C.
(1)若点A(0,6),N(0,2),∠ABN=30°,求点B的坐标;
(2)若D为线段NB的中点,求证:直线CD是⊙M的切线.
参考答案:
【答案】(1) B(![]() ,2).(2)证明见解析.
,2).(2)证明见解析.
【解析】
试题分析:(1)在Rt△ABN中,求出AN、AB即可解决问题;
(2)连接MC,NC.只要证明∠MCD=90°即可
试题解析:(1)∵A的坐标为(0,6),N(0,2),
∴AN=4,
∵∠ABN=30°,∠ANB=90°,
∴AB=2AN=8,
∴由勾股定理可知:NB=![]() ,
,
∴B(![]() ,2).
,2).
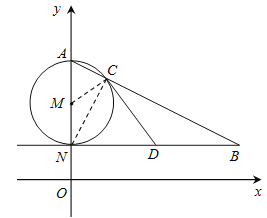
(2)连接MC,NC
∵AN是⊙M的直径,
∴∠ACN=90°,
∴∠NCB=90°,
在Rt△NCB中,D为NB的中点,
∴CD=![]() NB=ND,
NB=ND,
∴∠CND=∠NCD,
∵MC=MN,
∴∠MCN=∠MNC,
∵∠MNC+∠CND=90°,
∴∠MCN+∠NCD=90°,
即MC⊥CD.
∴直线CD是⊙M的切线.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列命题的逆命题是真命题的是( )
A. 对顶角相等 B. 如果两个角是直角那么这两个角相等
C. 全等三角形的对应角等 D. 两直线平行,内错角相等
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知线段AB,以下作图不可能的是( )
A. 在AB上取一点C,使AC=BC
B. 在AB的延长线上取一点C,使BC=AB
C. 在BA的延长线上取一点C,使BC=AB
D. 在BA的延长线上取一点C,使BC=2AB
-
科目: 来源: 题型:
查看答案和解析>>【题目】对于平面内任意一个四边形ABCD,现从以下四个关系式①AB=CD;②AD=BC;③AB∥CD;④∠A=∠C 中任取两个作为条件,能够得出这个四边形ABCD是平行四边形的组合是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】在直角三角形中,若一个锐角为35°,则另一个锐角为_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在﹣(﹣8),|﹣7|,﹣|0|,﹣(﹣3)2这四个数中,负数有( )
A.1个
B.2个
C.3个
D.4个 -
科目: 来源: 题型:
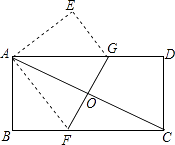
查看答案和解析>>【题目】如图,将一矩形纸片ABCD折叠,使两个顶点A,C重合,折痕为FG.若AB=4,BC=8,则△ABF的面积为 .
相关试题

