【题目】如图,将一矩形纸片ABCD折叠,使两个顶点A,C重合,折痕为FG.若AB=4,BC=8,则△ABF的面积为 . 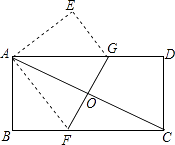
参考答案:
【答案】6
【解析】解:∵将一矩形纸片ABCD折叠,使两个顶点A,C重合,折痕为FG,
∴FG是AC的垂直平分线,
∴AF=CF,
设AF=FC=x,
在Rt△ABF中,有勾股定理得:AB2+BF2=AF2,
42+(8﹣x)2=x2,
解得:x=5,
即CF=5,BF=8﹣5=3,
∴△ABF的面积为 ![]() ×3×4=6,
×3×4=6,
所以答案是:6.
【考点精析】掌握翻折变换(折叠问题)是解答本题的根本,需要知道折叠是一种对称变换,它属于轴对称,对称轴是对应点的连线的垂直平分线,折叠前后图形的形状和大小不变,位置变化,对应边和角相等.
-
科目: 来源: 题型:
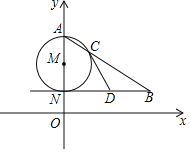
查看答案和解析>>【题目】如图,AN是⊙M的直径,NB∥x轴,AB交⊙M于点C.
(1)若点A(0,6),N(0,2),∠ABN=30°,求点B的坐标;
(2)若D为线段NB的中点,求证:直线CD是⊙M的切线.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在直角三角形中,若一个锐角为35°,则另一个锐角为_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在﹣(﹣8),|﹣7|,﹣|0|,﹣(﹣3)2这四个数中,负数有( )
A.1个
B.2个
C.3个
D.4个 -
科目: 来源: 题型:
查看答案和解析>>【题目】如果三角形三个外角度数之比为4:2:3,则这个三角形的各外角度数分别为________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:x5÷x2等于( )
A.x2B.x3C.2xD.2+x
-
科目: 来源: 题型:
查看答案和解析>>【题目】化简求值、解方程
(1)先化简(x+1﹣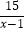 )÷
)÷  ,再取一个你认为合理的x值,代入求原式的值.
,再取一个你认为合理的x值,代入求原式的值.
(2)解方程: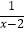 +3=
+3=  .
.
相关试题

