【题目】周末,老师带同学去北京植物园中的一二﹒九运动纪念广场,这里有三座侧面为三角形的纪念亭,挺拔的建筑线条象征青年朝气蓬勃、积极向上的精神.基于纪念亭的几何特征,同学们编拟了如下的数学问题:
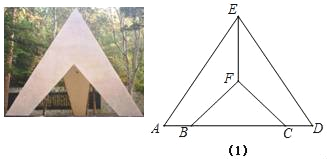
如图1,点A,B,C,D在同一条直线上,在四个论断“EA=ED,EF⊥AD,AB=DC,FB=FC”中选择三个作为已知条件,另一个作为结论,构成真命题(补充已知和求证),并进行证明.
已知:如图,点A,B,C,D在同一条直线上, .
求证: .
证明: .
参考答案:
【答案】见解析
【解析】
延长EF交BC于H,由EA=ED,EF⊥AD,
推出AH=HD,由AB=DC推出BH=CH,由FH⊥BC推出FB=FC;
由EA=ED,EF⊥AD推出AH=HD,由AB=DC,推出BH=CH,由FH⊥BC推出FB=FC.
解:已知:如图,EA=ED,EF⊥AD,AB=DC,求证FB=FC.
理由:延长EF交BC于H.
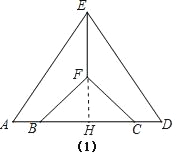
∵EA=ED,EF⊥AD,
∴AH=HD(等腰三角形三线合一),
∵AB=DC,
∴BH=CH,∵FH⊥BC,
∴FB=FC.
故答案为:EA=ED,EF⊥AD,AB=DC;FB=FC;
-
科目: 来源: 题型:
查看答案和解析>>【题目】某班数学兴趣小组对不等式组
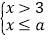 ,讨论得到以下结论:①若a=5,则不等式组的解集为3<x≤5;②若a=2,则不等式组无解;③若不等式组无解,则a的取值范围为a<3;④若不等式组只有两个整数解,则a的值可以为5.1,其中,正确的结论的序号是____.
,讨论得到以下结论:①若a=5,则不等式组的解集为3<x≤5;②若a=2,则不等式组无解;③若不等式组无解,则a的取值范围为a<3;④若不等式组只有两个整数解,则a的值可以为5.1,其中,正确的结论的序号是____. -
科目: 来源: 题型:
查看答案和解析>>【题目】关于x的不等式组
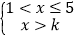
(1)不等式组有无数个解,
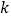 的取值范围是多少?
的取值范围是多少?(2)不等式组只有三个整数解,
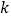 的取值范围是多少?
的取值范围是多少?(3)不等式组无解,
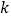 的取值范围是多少?
的取值范围是多少? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,矩形EFGH四个顶点分别在菱形ABCD的四条边上,BE=BF,将△AEH,△CFG分别沿边EH,FG折叠,当重叠部分为菱形且面积是菱形ABCD面积的
 时,则
时,则  为( )
为( )
A.
B.2
C.
D.4 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=BC,在BC上分别取点M、N,使MN=NA,若∠BAM=∠NAC,则∠MAC=_________°.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,矩形纸片ABCD中,AB=4,BC=6,将△ABC沿AC折叠,使点B落在点E处,CE交AD于点F,则DF的长等于( )
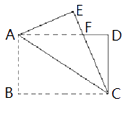
A.
B.
C.
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】随着某市教育改革的不断深入,素质教育的全面推进,中学生利用假期参加社会实践的调查越来越多,一位同学在A公司实习调查时,计划部给了他一份实习作业;在下述条件下,规划下个月的产量,若公司生产部有工人200名,每个工人的月劳动时间不超过196h,每个工人生产一件产品需用2h;本月将剩余原料60吨,下个月准备购进300吨,每件产品需原料20kg;经市场调查,预计下个月市场对这种产品的需求量不少于16000件,公司准备充分保证市场要求,你能和这位同学一同规划出下个月的产量范围吗?(设下个月产量为x件)
相关试题

