【题目】已知二次函数 ![]() 的图象与x轴交于A、B两点,点A的坐标为
的图象与x轴交于A、B两点,点A的坐标为 ![]() ,求点B的坐标.
,求点B的坐标.
参考答案:
【答案】解:∵二次函数 ![]() 的图象与x轴交于点A
的图象与x轴交于点A ![]() ,
,
∴ ![]() .
.
∴ ![]() .
.
∴二次函数解析式为 ![]() .
.
即 ![]() .
.
∴二次函数 ![]() 与x轴的交点B的坐标为
与x轴的交点B的坐标为 ![]() .
.
【解析】把点A坐标代入二次函数解析式,求出b的值,得到二次函数解析式,再用因式分解法,求出点B的坐标.
【考点精析】解答此题的关键在于理解抛物线与坐标轴的交点的相关知识,掌握一元二次方程的解是其对应的二次函数的图像与x轴的交点坐标.因此一元二次方程中的b2-4ac,在二次函数中表示图像与x轴是否有交点.当b2-4ac>0时,图像与x轴有两个交点;当b2-4ac=0时,图像与x轴有一个交点;当b2-4ac<0时,图像与x轴没有交点.
-
科目: 来源: 题型:
查看答案和解析>>【题目】湖南师大思沁新化实验学校是一所“高起点,高质量”的集团化民办名校,现有学生1000人(其中包括小学部和初中部),下学期计划扩招学生1500人,这样小学部人数增加了160%,初中部人数增加了135%,求扩招后该学校小学部和初中部各有多少名学生?
-
科目: 来源: 题型:
查看答案和解析>>【题目】图1是一个长为2m、宽为2n的长方形,沿图中虚线用剪刀均分成四块小长方形,然后按图2的形状拼成一下正方形.
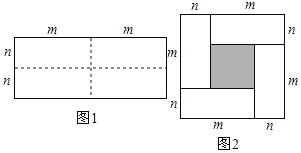
(1)请你用两种不同的方法求图2中阴影部分的面积?
① ②
(2)观察图2,写出三个代数式(m+n)2,(m﹣n)2,4mn之间的等量关系:
(3)根据(2)中的等量关系,解决如下问题:若|a+b﹣7|+|ab﹣6|=0,求(a﹣b)2的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC中,AB=6,AC=8,BC=10,P为边BC上一动点,PE⊥AB于E,PF⊥AC于F,M为EF中点,则AM的最小值为 .

-
科目: 来源: 题型:
查看答案和解析>>【题目】先化简,再求值:
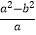 ÷(a﹣
÷(a﹣ 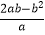 ),其中a=2+
),其中a=2+ 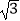 ,b=2﹣
,b=2﹣ 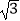 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】观察下列因式分解的过程:
(1)x2﹣xy+4x﹣4y
=(x2﹣xy)+(4x﹣4y)(分成两组)
=x(x﹣y)+4(x﹣y)直接提公因式)
=(x﹣y)(x+4)
(2)a2﹣b2﹣c2+2bc
=a2﹣(b2+c2﹣2bc)(分成两组)
=a2﹣(b﹣c)2(直接运用公式)
=(a+b﹣c)(a﹣b+c)
(1)请仿照上述分解因式的方法,把下列各式分解因式:
①
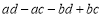
②
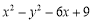
(2)请运用上述分解因式的方法,把多项式1+x+x(1+x)+x(1+x)2+…+x(1+x)n分解因式.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,把矩形纸片ABCD沿EF折叠,使点B落在边AD上的点B′处,点A落在点A′处;
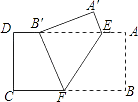
(1)求证:B′E=BF;
(2)设AE=a,AB=b,BF=c,试猜想a,b,c之间的一种关系,并给予证明.
相关试题

