【题目】如图,等圆⊙O1和⊙O2相交于A、B两点,⊙O1经过⊙O2的圆心,顺次连接A、O1、B、O2 . 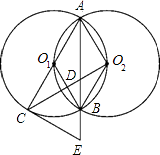
(1)求证:四边形AO1BO2是菱形;
(2)过直径AC的端点C作⊙O1的切线CE交AB的延长线于E,连接CO2交AE于D,求证:CE=2O2D;
(3)在(2)的条件下,若△AO2D的面积为1,求△BO2D的面积.
参考答案:
【答案】
(1)证明:∵⊙O1与⊙O2是等圆,
∴AO1=O1B=BO2=O2A,
∴四边形AO1BO2是菱形;
(2)证明:∵四边形AO1BO2是菱形,
∴∠O1AB=∠O2AB,
∵CE是⊙O1的切线,AC是⊙O1的直径,
∴∠ACE=∠AO2C=90°,
∴△ACE∽△AO2D,
![]() ,
,
即CE=2DO2;
(3)解:∵四边形AO1BO2是菱形,
∴AC∥BO2
∴△ACD∽△BO2D,
∴ ![]() ,
,
∴AD=2BD,
∵ ![]() ,
,
∴ ![]() ,
,

【解析】(1)根据⊙O1与⊙O2是等圆,可得AO1=O1B=BO2=O2A,利用四条边都相等的四边形是菱形可判定出结论;(2)根据已知得出△ACE∽△AO2D,进而得出 ![]() ,即可得出答案;(3)首先证明△ACD∽△BO2D,得出
,即可得出答案;(3)首先证明△ACD∽△BO2D,得出 ![]() ,AD=2BD,再利用等高不等底的三角形面积关系得出答案即可.
,AD=2BD,再利用等高不等底的三角形面积关系得出答案即可.
【考点精析】掌握菱形的判定方法和相交两圆的性质是解答本题的根本,需要知道任意一个四边形,四边相等成菱形;四边形的对角线,垂直互分是菱形.已知平行四边形,邻边相等叫菱形;两对角线若垂直,顺理成章为菱形;相交的两个圆的连心线垂直平分两圆的公共弦.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,是一台自动测温仪记录的图象,它反映了我市冬季某天气温T随时间t变化而变化的关系,观察图象得到下列信息,其中错误的是( )

A. 凌晨4时气温最低为-3℃
B. 14时气温最高为8℃
C. 从0时至14时,气温随时间增长而上升
D. 从14时至24时,气温随时间增长而下降
-
科目: 来源: 题型:
查看答案和解析>>【题目】李明到离家2.1千米的学校参加初三联欢会,到学校时发现演出道具还放在家中,此时距联欢会开始还有42分钟,于是他立即匀速步行回家,在家拿道具用了1分钟,然后立即匀速骑自行车返回学校.已知李明骑自行车到学校比他从学校步行到家用时少20分钟,且骑自行车的速度是步行速度的3倍.
(1)李明步行的速度(单位:米/分)是多少?
(2)李明能否在联欢会开始前赶到学校? -
科目: 来源: 题型:
查看答案和解析>>【题目】一食堂需要购买盒子存放食物,盒子有A,B两种型号,单个盒子的容量和价格如表.
型号
A
B
单个盒子容量(升)
2
3
单价(元)
5
6
现有15升食物需要存放且要求每个盒子要装满,由于A型号盒子正做促销活动:购买三个及三个以上可一次性返还现金4元,则购买盒子所需要最少费用为________元.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠BAC=90°,AB=AC=6,D为BC的中点.
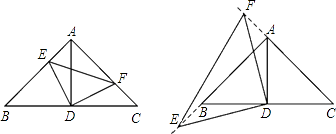
(1)若E、F分别是AB、AC上的点,且AE=CF,求证:△AED≌△CFD;
(2)当点F、E分别从C、A两点同时出发,以每秒1个单位长度的速度沿CA、AB运动,到点A、B时停止;设△DEF的面积为y,F点运动的时间为x,求y与x的函数关系式;
(3)在(2)的条件下,点F、E分别沿CA、AB的延长线继续运动,求此时y与x的函数关系式. -
科目: 来源: 题型:
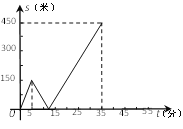
查看答案和解析>>【题目】甲乙两人匀速从同一地点到1500米处的图书馆看书,甲出发5分钟后,乙以50米/分的速度沿同一路线行走.设甲乙两人相距
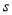 (米),甲行走的时间为
(米),甲行走的时间为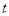 (分),
(分),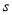 关于
关于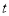 的函数函数图像的一部分如图所示.
的函数函数图像的一部分如图所示.(1)求甲行走的速度;
(2)在坐标系中,补画
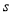 关于
关于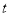 函数图象的其余部分;
函数图象的其余部分;(3)问甲、乙两人何时相距360米?
-
科目: 来源: 题型:
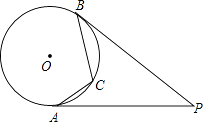
查看答案和解析>>【题目】如图,PA、PB是⊙O的切线,A、B是切点,点C是劣弧AB上的一个动点,若∠P=40°,则∠ACB的度数是( )
A.80°
B.110°
C.120°
D.140°
相关试题

