搜索
【题目】解下列不等式（组）
（1）0.01x﹣1≥0.02x；
（2）
；
（3）
；
（4）
．
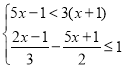参考答案：
【答案】（1）x≤﹣100；（2）x＞
；（3）x＜
；（4）﹣1≤x＜2．
【解析】
（1）先移项、合并同类项，再系数化为1即可得；
（2）先去分母，再移项、合并同类项、系数化为1即可得；
（3）先通过移项、合并同类项、系数化为1分别求出两个不等式的解，再找出其公共部分即可得不等式组的解集；
（4）先通过去分母、去括号、移项、合并同类项、系数化为1分别求出两个不等式的解，再找出其公共部分即可得不等式组的解集．
（1）
；
（2）
；
（3）不等式
移项、合并同类项，得
系数化为1，得
不等式
移项、合并同类项，得
系数化为1，得
故不等式组的解集为；
（4）不等式
去括号，得
移项、合并同类项，得
系数化为1，得
不等式
去分母，得
去括号，得
移项、合并同类项，得
系数化为1，得
故不等式组的解集为
．
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知，点A（1，﹣
），点B（﹣2，n）在抛物线y=ax2（a≠0）上．（1）求a的值与点B的坐标；
（2）将抛物线y=ax2（a≠0）平移，记平移后点A的对应点为A′，点B的对应点为B'，若四边形ABB′A′为正方形，求平移后的抛物线的解析式．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，若△ABC内一点P满足∠PAC=∠PCB=∠PBA，则称点P为△ABC的布罗卡尔点，三角形的布罗卡尔点是法国数学家和数学教育家克雷尔首次发现，后来被数学爱好者法国军官布罗卡尔重新发现，并用他的名字命名，布罗卡尔点的再次发现，引发了研究“三角形几何”的热潮．已知△ABC中，CA=CB，∠ACB=120°，P为△ABC的布罗卡尔点，若PA=
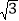，则PB+PC=_____．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在平面直角坐标系中，直线y=﹣
x﹣1分别交x轴、y轴于点A、B，在第二象限内有一边长为2的正方形CDEF，已知C（﹣1，1），若动点P从C出发以每秒1个单位的速度沿着正方形CDEF的边逆时针运动一周（到达C点后停止运动），设P点运动的时间为t秒．（1）是否存在t，使得以P为圆心，
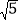为半径的圆与直线AB相切？若存在，求出所有t的值；若存在，请说明理由．（2）在点P运动的同时，直线AB以每秒1个单位的速度向右作匀速运动（与点P同时停止）是否存在t，使得以P为圆心，
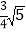为半径的圆与平移后的直线A′B′相切？请直接写出所有t的值．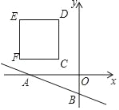
-
科目： 来源： 题型：
查看答案和解析>>【题目】某校九年级10个班师生举行毕业文艺汇演，每班2个节目，有歌唱与舞蹈两类节目，年级统计后发现歌唱类节目数比舞蹈类节目数的2倍少4个.
（1）九年级师生表演的歌唱与舞蹈类节目数各有多少个？
（2）该校七、八年级师生有小品节目参与，在歌唱、舞蹈、小品三类节目中，每个节目的演出平均用时分别是5分钟、6分钟、8分钟，预计所有演出节目交接用时共花15分钟.若从20：00开始，22：30之前演出结束，问参与的小品类节目最多能有多少个？
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，AC是⊙O的直径，弦BD⊥AO于E，连接BC，过点O作OF⊥BC于F，若BD=8cm，AE=2cm，则OF的长度是（ ）
A. 3cm B.
cm C. 2.5cm D. 
cm -
科目： 来源： 题型：
查看答案和解析>>【题目】如图，AB是圆O的直径，C、D是圆O上的点，且OC∥BD，AD分别与BC、OC相交于点E、F．则下列结论：
①AD⊥BD；②∠AOC=∠ABC；③CB平分∠ABD；④AF=DF；⑤BD=2OF．
其中一定成立的是（ ）
A．①③⑤ B．②③④ C．②④⑤ D．①③④⑤
相关试题
