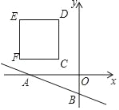
【题目】如图,在平面直角坐标系中,直线y=﹣![]() x﹣1分别交x轴、y轴于点A、B,在第二象限内有一边长为2的正方形CDEF,已知C(﹣1,1),若动点P从C出发以每秒1个单位的速度沿着正方形CDEF的边逆时针运动一周(到达C点后停止运动),设P点运动的时间为t秒.
x﹣1分别交x轴、y轴于点A、B,在第二象限内有一边长为2的正方形CDEF,已知C(﹣1,1),若动点P从C出发以每秒1个单位的速度沿着正方形CDEF的边逆时针运动一周(到达C点后停止运动),设P点运动的时间为t秒.
(1)是否存在t,使得以P为圆心,![]() 为半径的圆与直线AB相切?若存在,求出所有t的值;若存在,请说明理由.
为半径的圆与直线AB相切?若存在,求出所有t的值;若存在,请说明理由.
(2)在点P运动的同时,直线AB以每秒1个单位的速度向右作匀速运动(与点P同时停止)是否存在t,使得以P为圆心,![]() 为半径的圆与平移后的直线A′B′相切?请直接写出所有t的值.
为半径的圆与平移后的直线A′B′相切?请直接写出所有t的值.
参考答案:
【答案】(1)满足条件的t的值为1或4.(2)满足条件的t的值为![]() 或
或![]() 或
或![]() .
.
【解析】
(1) 设存在点P.作PH⊥AB,PM⊥x轴交AB于Q,可证△PHQ∽△AOB,可得PQ=![]() ,分点P在CD上时,与当点P在DE上时讨论,可得t的值;
,分点P在CD上时,与当点P在DE上时讨论,可得t的值;
(2)由题意平移后可得直线A′B′的解析式为,作PH⊥A′B′,PM⊥x轴交A′B′于Q.当PH=![]()
![]() 时,同法可得PQ=
时,同法可得PQ=![]() ,分①当点P在CD上时,②当点P在DE上时,
,分①当点P在CD上时,②当点P在DE上时,
③当点P在EF上时,三种情况讨论,可的t的值.
解:(1)假设存在点P.作PH⊥AB,PM⊥x轴交AB于Q.

∵PQ∥y轴,
∴∠OBA=∠PQH,
∵∠AOB=∠PHQ=Rt∠,
∴△PHQ∽△AOB,
∴![]() =
=![]() ,
,
∵A(﹣1,2)或(﹣3,3),PH=![]() ,
,
∴AO=2,AB=![]() ,
,
∴PQ=![]() ,
,
①当点P在CD上时,t+1+![]() =
=![]() ,解得t=1,
,解得t=1,
②当点P在DE上时,3﹣[﹣![]() (1﹣t)﹣1]=
(1﹣t)﹣1]=![]() ,解得t=4,此时点P与E重合.
,解得t=4,此时点P与E重合.
综上所述,满足条件的t的值为1或4.
(2)由题意平移后的直线A′B′的解析式为y=﹣![]() x﹣1+
x﹣1+![]() ,
,
作PH⊥A′B′,PM⊥x轴交A′B′于Q.
当PH=![]()
![]() 时,同法可得PQ=
时,同法可得PQ=![]() ,
,
①当点P在CD上时,1+t﹣(![]() ﹣1+
﹣1+![]() )=
)=![]() ,解得t=
,解得t=![]() ,
,
②当点P在DE上时,3﹣[﹣![]() (1﹣t)﹣1+
(1﹣t)﹣1+![]() ]=
]=![]() ,解得t=
,解得t=![]() ,
,
③当点P在EF上时,![]() ﹣1+
﹣1+![]() ﹣(6﹣t+1)=
﹣(6﹣t+1)=![]() ,解得t=
,解得t=![]() ,
,
综上所述,满足条件的t的值为![]() 或
或![]() 或
或![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】宜兴在“创建文明城市”行动中,某社区计划对面积为2160m2的区域进行绿化.经投标,由甲、乙两个工程队来完成,已知甲队每天能完成绿化的面积是乙队每天能完成绿化面积的2倍,并且在独立完成面积为480m2区域的绿化时,甲队比乙队少用4天.
(1)求甲、乙两工程队每天能完成绿化的面积;
(2)设甲工程队施工x天,乙工程队施工y天,刚好完成绿化任务,求y与x的函数表达式;
(3)若甲队每天绿化费用是0.8万元,乙队每天绿化费用为0.35万元,且甲、乙两队施工的总天数不超过26天,则如何安排甲乙两队施工的天数,使施工总费用最低?并求出最低费用.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知,点A(1,﹣
 ),点B(﹣2,n)在抛物线y=ax2(a≠0)上.
),点B(﹣2,n)在抛物线y=ax2(a≠0)上.(1)求a的值与点B的坐标;
(2)将抛物线y=ax2(a≠0)平移,记平移后点A的对应点为A′,点B的对应点为B',若四边形ABB′A′为正方形,求平移后的抛物线的解析式.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,若△ABC内一点P满足∠PAC=∠PCB=∠PBA,则称点P为△ABC的布罗卡尔点,三角形的布罗卡尔点是法国数学家和数学教育家克雷尔首次发现,后来被数学爱好者法国军官布罗卡尔重新发现,并用他的名字命名,布罗卡尔点的再次发现,引发了研究“三角形几何”的热潮.已知△ABC中,CA=CB,∠ACB=120°,P为△ABC的布罗卡尔点,若PA=
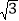 ,则PB+PC=_____.
,则PB+PC=_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】解下列不等式(组)
(1)0.01x﹣1≥0.02x;
(2)
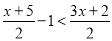 ;
;(3)
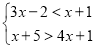 ;
;(4)
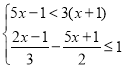 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】某校九年级10个班师生举行毕业文艺汇演,每班2个节目,有歌唱与舞蹈两类节目,年级统计后发现歌唱类节目数比舞蹈类节目数的2倍少4个.
(1)九年级师生表演的歌唱与舞蹈类节目数各有多少个?
(2)该校七、八年级师生有小品节目参与,在歌唱、舞蹈、小品三类节目中,每个节目的演出平均用时分别是5分钟、6分钟、8分钟,预计所有演出节目交接用时共花15分钟.若从20:00开始,22:30之前演出结束,问参与的小品类节目最多能有多少个?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AC是⊙O的直径,弦BD⊥AO于E,连接BC,过点O作OF⊥BC于F,若BD=8cm,AE=2cm,则OF的长度是( )

A. 3cm B.
 cm C. 2.5cm D.
cm C. 2.5cm D.  cm
cm
相关试题

