【题目】如图,若△ABC内一点P满足∠PAC=∠PCB=∠PBA,则称点P为△ABC的布罗卡尔点,三角形的布罗卡尔点是法国数学家和数学教育家克雷尔首次发现,后来被数学爱好者法国军官布罗卡尔重新发现,并用他的名字命名,布罗卡尔点的再次发现,引发了研究“三角形几何”的热潮.已知△ABC中,CA=CB,∠ACB=120°,P为△ABC的布罗卡尔点,若PA=![]() ,则PB+PC=_____.
,则PB+PC=_____.

参考答案:
【答案】1+![]() .
.
【解析】
作CH⊥AB于H.首先证明BC=![]() BC,再证明△PAB∽△PBC,可得
BC,再证明△PAB∽△PBC,可得![]() ,即可求出PB、PC.
,即可求出PB、PC.
作CH⊥AB于H.
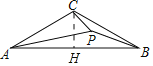
∵CA=CB,CH⊥AB,∠ACB=120°,
∴AH=BH,∠ACH=∠BCH=60°,∠CAB=∠CBA=30°,
∴AB=2BH=2BCcos30°=![]() BC,
BC,
∵∠PAC=∠PCB=∠PBA,
∴∠PAB=∠PBC,
∴△PAB∽△PBC,
∴![]() ,
,
∵PA=![]() ,
,
∴PB=1,PC=![]() ,
,
∴PB+PC=1+![]() .
.
故答案为1+![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某数学兴趣小组在全校范围内随机抽取了50名同学进行“舌尖上的宜兴﹣我最喜爱的宜兴小吃”调查活动,将调查问卷整理后绘制成如图所示的不完整条形统计图.
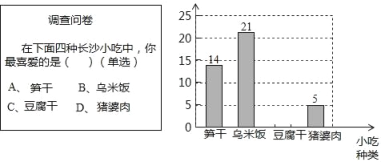
请根据所给信息解答以下问题
(1)请补全条形统计图;
(2)若全校有1000名同学,请估计全校同学中最喜爱“笋干”的同学有多少人?
(3)在一个不透明的口袋中有4个元全相同的小球,把它们分别标号为四种小吃的序号A,B,C,D,随机地把四个小球分成两组,每组两个球,请用列表或画树状图的方法,求出A,B两球分在同一组的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】宜兴在“创建文明城市”行动中,某社区计划对面积为2160m2的区域进行绿化.经投标,由甲、乙两个工程队来完成,已知甲队每天能完成绿化的面积是乙队每天能完成绿化面积的2倍,并且在独立完成面积为480m2区域的绿化时,甲队比乙队少用4天.
(1)求甲、乙两工程队每天能完成绿化的面积;
(2)设甲工程队施工x天,乙工程队施工y天,刚好完成绿化任务,求y与x的函数表达式;
(3)若甲队每天绿化费用是0.8万元,乙队每天绿化费用为0.35万元,且甲、乙两队施工的总天数不超过26天,则如何安排甲乙两队施工的天数,使施工总费用最低?并求出最低费用.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知,点A(1,﹣
 ),点B(﹣2,n)在抛物线y=ax2(a≠0)上.
),点B(﹣2,n)在抛物线y=ax2(a≠0)上.(1)求a的值与点B的坐标;
(2)将抛物线y=ax2(a≠0)平移,记平移后点A的对应点为A′,点B的对应点为B',若四边形ABB′A′为正方形,求平移后的抛物线的解析式.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,直线y=﹣
 x﹣1分别交x轴、y轴于点A、B,在第二象限内有一边长为2的正方形CDEF,已知C(﹣1,1),若动点P从C出发以每秒1个单位的速度沿着正方形CDEF的边逆时针运动一周(到达C点后停止运动),设P点运动的时间为t秒.
x﹣1分别交x轴、y轴于点A、B,在第二象限内有一边长为2的正方形CDEF,已知C(﹣1,1),若动点P从C出发以每秒1个单位的速度沿着正方形CDEF的边逆时针运动一周(到达C点后停止运动),设P点运动的时间为t秒.(1)是否存在t,使得以P为圆心,
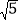 为半径的圆与直线AB相切?若存在,求出所有t的值;若存在,请说明理由.
为半径的圆与直线AB相切?若存在,求出所有t的值;若存在,请说明理由.(2)在点P运动的同时,直线AB以每秒1个单位的速度向右作匀速运动(与点P同时停止)是否存在t,使得以P为圆心,
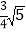 为半径的圆与平移后的直线A′B′相切?请直接写出所有t的值.
为半径的圆与平移后的直线A′B′相切?请直接写出所有t的值.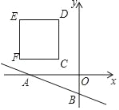
-
科目: 来源: 题型:
查看答案和解析>>【题目】解下列不等式(组)
(1)0.01x﹣1≥0.02x;
(2)
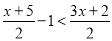 ;
;(3)
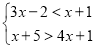 ;
;(4)
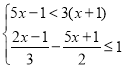 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】某校九年级10个班师生举行毕业文艺汇演,每班2个节目,有歌唱与舞蹈两类节目,年级统计后发现歌唱类节目数比舞蹈类节目数的2倍少4个.
(1)九年级师生表演的歌唱与舞蹈类节目数各有多少个?
(2)该校七、八年级师生有小品节目参与,在歌唱、舞蹈、小品三类节目中,每个节目的演出平均用时分别是5分钟、6分钟、8分钟,预计所有演出节目交接用时共花15分钟.若从20:00开始,22:30之前演出结束,问参与的小品类节目最多能有多少个?
相关试题

