【题目】如图,正方形ABCD的对角线相交于点O,点O也是正方形A′B′C′O的一个顶点,两个正方形的边长都等于1,当正方形A′B′C′O绕顶点O转动时,两个正方形重叠部分的面积大小有什么规律?并说明理由.

参考答案:
【答案】两个正方形重叠部分的面积保持不变,始终为![]() .
.
理由:∵四边形ABCD是正方形,
∴OB=OC,∠OBE=∠OCF=45°,∠BOC=90°.
∵四边形A′B′C′O是正方形,
∴∠EOF=90°,∴∠BOC=∠EOF.
∴∠BOC-∠BOF=∠EOF-∠BOF,
即∠COF=∠BOE.
∴△BOE≌△COF(ASA),
∴S△BOE=S△COF.
∴重叠部分面积等于S△BOC.
∵S正方形ABCD=1×1=1,
∴![]() ,即两个正方形重叠部分的面积保持不变,始终为
,即两个正方形重叠部分的面积保持不变,始终为![]() .
.
【解析】正方形的两条对角线分正方形为四个全等的等腰直角三角形.通过证△BOE≌△COF,得![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某工厂对一批产品进行了抽样检测.右图是根据抽样检测后的产品净重(单位:克)数据绘制的频率分布直方图,其中产品净重的范围是[96,106](即96≤净重≤106),样本数据分组为[96,98)(即96≤净重<98)以下类似,[98,100),[100,102),[102,104),[104,106],已知样本中产品净重小于100克的个数是36,则样本中净重大于或等于98克并且小于104克的产品的个数是 ( ).
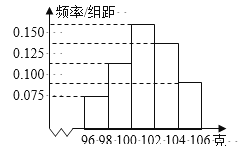
A.90
B.75
C.60
D.45 -
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法正确的是( )
A. 相似三角形一定全等B. 不相似的三角形不一定全等
C. 全等三角形不一定是相似三角形D. 全等三角形一定是相似三角形
-
科目: 来源: 题型:
查看答案和解析>>【题目】互联网“微商”经营已成为大众创业新途径,某微信平台上一件商品进价200元,按标价的五折销售,仍可获利10%,设这件商品的标价为_____元.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为响应市教育局倡导的“阳光体育运动”的号召,全校学生积极参与体育运动.为了进一步了解学校九年级学生的身体素质情况,体育老师在九年级800名学生中随机抽取50位学生进行一分钟跳绳次数测试,以测试数据为样本,绘制出部分频数分布表和部分频数分布直方图,如下所示:
组别
次数x
频数(人数)
第1组
80≤x<100
6
第2组
100≤x<120
8
第3组
120≤x<140
a
第4组
140≤x<160
18
第5组
160≤x<180
6
请结合图表完成下列问题:
(1)表中的a=;
(2)请把频数分布直方图补充完整;
(3)这个样本数据的中位数落在第组;
(4)若九年级学生一分钟跳绳次数(x)达标要求是:x<120为不合格;120≤x<140为合格;140≤x<160为良;x≥160为优.根据以上信息,请你估算学校九年级同学一分钟跳绳次数为优的人数为 . -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在矩形ABCD中,点E在边CD上,将该矩形沿AE折叠,使点D落在边BC上的点F处,过点F作FG∥CD,交AE于点G,连接DG.

(1)求证:四边形DEFG为菱形;
(2)若CD=8,CF=4,求
 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知二次函数y=ax2+bx+c(a≠0)的图象与x轴交于点A(﹣1,0),与y轴的交点B在(0,﹣2)和(0,﹣1)之间(不包括这两点),对称轴为直线x=1.下列结论:①abc>0 ②4a+2b+c>0 ③4ac﹣b2<8a ④
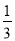 <a<
<a<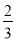 ⑤b>c.其中含所有正确结论的选项是( )
⑤b>c.其中含所有正确结论的选项是( )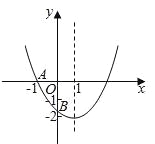
A.①③ B.①③④ C.②④⑤ D.①③④⑤
相关试题

