【题目】(满分10分)有一个不透明口袋,装有分别标有数字1,2,3,4的4个小球(小球除数字不同外,其余都相同),另有3张背面完全一样、正面分别写有数字1,2,3的卡片.小敏从口袋中任意摸出一个小球,小颖从这3张背面朝上的卡片中任意摸出一张,然后计算小球和卡片上的两个数的积.
(1)请你求出摸出的这两个数的积为6的概率;
(2)小敏和小颖做游戏,她们约定:若这两个数的积为奇数,小敏赢;否则,小颖赢.你认为该游戏公平吗?为什么?如果不公平,请你修改游戏规则,使游戏公平.
参考答案:
【答案】(本题10分)解:(1)当小敏摸到标有数字1的小球时,小颖摸到的卡片可能标有1或2或3,积为1或2或3;当小敏摸到标有数字2的小球时,小颖摸到的卡片可能标有1或2或3,积为2或4或6;当小敏摸到标有数字3的小球时,小颖摸到的卡片可能标有1或2或3,积为3或6或9;当小敏摸到标有数字4的小球时,小颖摸到的卡片可能标有1或2或3,积为4或8或12。总结果有12种,其中积为6的有2种,∴摸出的这两个数的积为6的概率是![]() . ………………………………5分
. ………………………………5分
(2)游戏不公平,因为积为偶数的有8种情况,而积为奇数的有4种情况.…………7分
游戏规则可改为:若积为3的倍数,小敏赢,否则,小颖赢. ………10分
注:修改游戏规则,应不改变已知数字和小球、卡片数量.其他规则,凡正确均给分。
【解析】
解:(1)列表如下:
| 1 | 2 | 3 | 4 |
1 | 1 | 2 | 3 | 4 |
2 | 2 | 4 | 6 | 8 |
3 | 3 | 6 | 9 | 12 |
………………………………………………………(2分)
总结果有12种,其中积为6的有2种,
∴P(积为6)=![]() . ………………………………………(4分)
. ………………………………………(4分)
(2)游戏不公平,因为积为偶数的有8种情况,而积为奇数的有4种情况.(6分)
游戏规则可改为:若积为3的倍数,小敏赢,否则,小颖赢. ………(8
注:修改游戏规则,应不改变已知数字和小球、卡片数量.其他规则,凡正确均给分.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在一次数学兴趣小组活动中,李燕和刘凯两位同学设计了如图所示的两个转盘做游戏(每个转盘被分成面积相等的几个扇形,并在每个扇形区域内标上数字).游戏规则如下:两人分别同时转动甲、乙转盘,转盘停止后,若指针所指区域内两数和小于12,则李燕获胜;若指针所指区域内两数和等于12,则为平局;若指针所指区域内两数和大于12,则刘凯获胜(若指针停在等分线上,重转一次,直到指针指向某一份内为止).

(1)请用列表的方法表示出上述游戏中两数和的所有可能的结果;
(2)分别求出李燕和刘凯获胜的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,平面直角坐标系中,ABCD为长方形,其中点A、C坐标分别为(﹣4,2)、(1,﹣4),且AD∥x轴,交y轴于M点,AB交x轴于N.
(1)求B、D两点坐标和长方形ABCD的面积;
(2)一动点P从A出发(不与A点重合),以
 个单位/秒的速度沿AB向B点运动,在P点运动过程中,连接MP、OP,请直接写出∠AMP、∠MPO、∠PON之间的数量关系;
个单位/秒的速度沿AB向B点运动,在P点运动过程中,连接MP、OP,请直接写出∠AMP、∠MPO、∠PON之间的数量关系;(3)是否存在某一时刻t,使三角形AMP的面积等于长方形面积的
 ?若存在,求t的值并求此时点P的坐标;若不存在请说明理由.
?若存在,求t的值并求此时点P的坐标;若不存在请说明理由.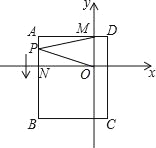
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在
 中,
中, ,点
,点 在
在 边上,点
边上,点 在
在 边上,且
边上,且 ,连接
,连接 .
.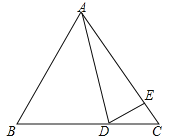
(1)当
 时,求
时,求 的度数
的度数(2)当点
 在
在 (点
(点 、
、 除外)边上运动,试写出
除外)边上运动,试写出 与
与 的数量关系,并说明理由
的数量关系,并说明理由 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知∠1=∠2,∠B=∠C,可推得AB∥CD.理由如下:
∵∠1=∠2(已知),
且∠1=∠CGD( ),
∴∠2=∠CGD(等量代换),
∴CE∥BF( ),
∴∠ =∠BFD( ).
又∵∠ =∠C(已知),
∴∠BFD=∠B(等量代换),
∴AB∥CD( ).
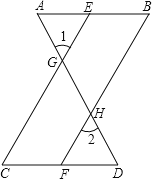
-
科目: 来源: 题型:
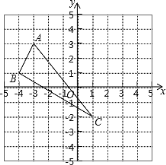
查看答案和解析>>【题目】在平面直角坐标系中,△ABC三个顶点的位置如图(每个小正方形的边长均为1):
(1)请画出△ABC沿
 轴向右平移3个单位长度,再沿
轴向右平移3个单位长度,再沿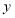 轴向上平移2个单位长度后的
轴向上平移2个单位长度后的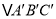 (其中
(其中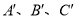 分别是A、B、C的对应点,不写画法);
分别是A、B、C的对应点,不写画法);(2)直接写出
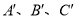 三点的坐标;
三点的坐标;(3)求△ABC的面积.
-
科目: 来源: 题型:
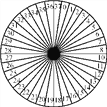
查看答案和解析>>【题目】转盘被均匀分为37格,分别标以0~36这37个数字,且所有写有偶数(0除外)的格子都涂成了红色,写有奇数的格子都涂成了蓝色,而0所在的格子被涂成了绿色.游戏者用此转盘(如图)做游戏,每次游戏游戏者交游戏费1元,游戏时,游戏者先押一个数字,然后快速地转动转盘,若转盘停止转动时,指针所指格子中的数字恰为游戏者所押数字,则游戏者将获得奖励36元,该游戏对游戏者有利吗?转动多次后,游戏者平均每次将获得或损失多少元?
相关试题


