【题目】随着人民生活水平的提高,汽车进入家庭的越来越多.我市某小区在2007年底拥有家庭轿车64辆,到了2009年底,家庭轿车数为100辆.
(1)若平均每年轿车数的增长率相同,求这个增长率.
(2)为了缓解停车矛盾,多增加一些车位,该小区决定投资15万元,再造一些停车位.据测算,建造一个室内停车位,需5000元;建造一个室外停车位,需1000元.按实际情况考虑,计划室外停车位数不少于室内车位的2倍,又不能超过室内车位的2.5倍.问,该小区有哪几种建造方案?应选择哪种方案最合理?
参考答案:
【答案】(1)25%;(2)选择方案①更合理.
【解析】试题分析:(1)2007年底拥有家庭轿车的辆数×(1+增长率)2=2009年底家庭轿车数,把相关数值代入计算即可;
(2)关系式为:室内停车位需投资+室外停车位投资=150000;室内车位的2倍≤室外停车位数≤室内车位的2.5倍,用室内车位数表示出室外车位数,代入不等式求解后找到整数解即可找到相应方案;找到车位数较多的方案即为合理方案.
试题解析:(1)设年增长率为x.
64(1+x)2=100
∴![]() ;
;
∴年增长率为25%;
(2)设造室内停车位x个,室外停车位y个
![]() ;
;
由①得,y=150﹣5x③,
把③代入②得:![]() ,
,
解得![]() ;
;
∴![]() 或
或![]() .
.
∴有两种方案:①室内20个,室外50个;②或室内21个,室外45个.
①方案中车位总数较多,选择方案①更合理.
-
科目: 来源: 题型:
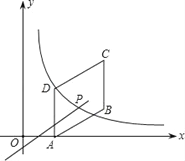
查看答案和解析>>【题目】如图,四边形ABCD是平行四边形,点A(1,0),B(4,1),C(4,3),反比例函数y=
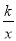 的图象经过点D,点P是一次函数y=mx+3﹣4m(m≠0)的图象与该反比例函数图象的一个公共点;
的图象经过点D,点P是一次函数y=mx+3﹣4m(m≠0)的图象与该反比例函数图象的一个公共点;(1)求反比例函数的解析式;
(2)通过计算说明一次函数y=mx+3﹣4m的图象一定过点C;
(3)对于一次函数y=mx+3﹣4m(m≠0),当y随x的增大而增大时,确定点P的横坐标的取值范围,(不必写过程)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,函数
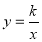 的图象与函数
的图象与函数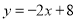 的图象交于点
的图象交于点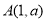 ,
,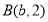 .
.(1)求函数
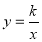 的表达式;
的表达式;(2)观察图象,直接写出不等式
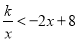 的解集;
的解集;(3)若点
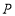 是
是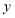 轴上的动点,当
轴上的动点,当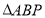 周长最小时,求点
周长最小时,求点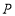 的坐标.
的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某国际化学校实行小班制教学,七年级四个班共有学生(6m-3n)人,一班有学生m人,二班人数比一班人数的两倍少n人,三班人数比二班人数的一半多12人.
(1)求三班的学生人数(用含m.n的式子表示);
(2)求四班的学生人数;(用含m.n的式子表示);
(3)若四个班共有学生120人,求二班比三班多的学生人数?
-
科目: 来源: 题型:
查看答案和解析>>【题目】某市区自2014年1月起,居民生活用水开始实行阶梯式计量水价,该阶梯式计量水价分为三级(如下表所示):
月用水量(吨)
水价(元/吨)
第一级 20吨以下(含20吨)
1.6
第二级 20吨﹣30吨(含30吨)
2.4
第三级 30吨以上
3.2
例:某用户的月用水量为32吨,按三级计量应缴水费为:
1.6×20+2.4×10+3.2×2=62.4(元)
(1)如果甲用户的月用水量为12吨,则甲需缴的水费为 元;
(2)如果乙用户缴的水费为39.2元,则乙月用水量 吨;
(3)如果丙用户的月用水量为a吨,则丙用户该月应缴水费多少元?(用含a的代数式表示,并化简)
-
科目: 来源: 题型:
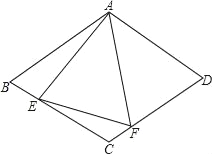
查看答案和解析>>【题目】如图,在菱形ABCD中,AB=4,∠BAD=120°,△AEF为正三角形,E、F在菱形的边BC,CD上.
(1)证明:BE=CF.
(2)当点E,F分别在边BC,CD上移动时(△AEF保持为正三角形),请探究四边形AECF的面积是否发生变化?若不变,求出这个定值;如果变化,求出其最大值.
(3)在(2)的情况下,请探究△CEF的面积是否发生变化?若不变,求出这个定值;如果变化,求出其最大值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一辆出租车从
 地出发,在一条东西走向的街道上往返,每次行驶的路程(记向东为正)记录如下表所示(
地出发,在一条东西走向的街道上往返,每次行驶的路程(记向东为正)记录如下表所示( ,单位:
,单位: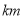 )
)第一次
第二次
第三次
第四次
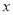
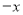
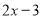
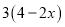
(1)写出这辆出租车每次行驶的方向.
(2)求经过连续4次行驶后,这辆出租车所在的位置.
(3)这辆出租车一共行驶多少路程?
相关试题

