【题目】用正方形使纸板做三棱柱盒子,每个盒子由3个长方形侧面和2个正三角形底面组成.硬纸板以如图两种方法裁剪(裁剪后边角料不再利用)). A方法:剪6个侧面;
B方法:剪4个侧面和5个底面.
现有19张硬纸板,裁剪时x张用A方法,其余用B方法.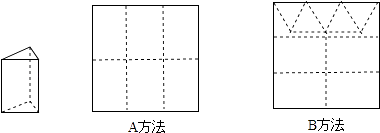
(1)分别求裁剪出的侧面和底面的个数(用x的代数式表示)
(2)若裁剪出的侧面和底面恰好全部用完,问能做多少个盒子?
参考答案:
【答案】
(1)解:∵裁剪时x张用A方法,
∴裁剪时(19﹣x)张用B方法.
∴侧面的个数为:6x+4(19﹣x)=(2x+76)个,
底面的个数为:5(19﹣x)=(95﹣5x)个
(2)解:由题意,得(2x+76):(95﹣5x)=3:2,
解得:x=7,
∴盒子的个数为: ![]() =30.
=30.
答:裁剪出的侧面和底面恰好全部用完,能做30个盒子
【解析】(1)由x张用A方法,就有(19﹣x)张用B方法,就可以分别表示出侧面个数和底面个数;(2)由侧面个数和底面个数比为3:2建立方程求出x的值,求出侧面的总数就可以求出结论.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若﹣x3ya与xby是同类项,则a+b的值为( )
A.5
B.4
C.3
D.2 -
科目: 来源: 题型:
查看答案和解析>>【题目】一元二次方程kx2+4x+1=0有两个实数根,则k的取值范围是( )
A. k>4B. k≥4C. k≤4D. k≤4且k≠0
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,∠AOE=90°,∠BOD=45°,那么图中不大于90°的角有个,它们的度数之和是°.
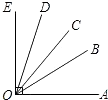
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,ABCD中,E、F分别是边AB、CD的中点.
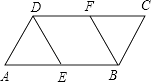
(1)求证:四边形EBFD是平行四边形;
(2)若AD=AE=2,∠A=60°,求四边形EBFD的周长. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知数轴上的点A表示的数为6,点B表示的数为﹣4,点C到点A、点B的距离相等,动点P从点B出发,以每秒2个单位长度的速度沿数轴向右匀速运动,设运动时间为 x ( x 大于0)秒.
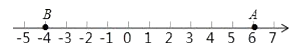
(1)点C表示的数是;
(2)当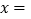 秒时,点P到达点A处?
秒时,点P到达点A处?
(3)运动过程中点P表示的数是(用含字母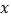 的式子表示);
的式子表示);
(4)当P,C之间的距离为2个单位长度时,求 x 的值. -
科目: 来源: 题型:
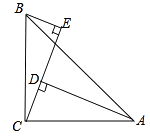
查看答案和解析>>【题目】如图,在△ABC中,∠ACB=90°,AC=BC , BE⊥CE于点E . AD⊥CE于点D.求证:△BEC≌△CDA.
相关试题

