【题目】如图,已知数轴上的点A表示的数为6,点B表示的数为﹣4,点C到点A、点B的距离相等,动点P从点B出发,以每秒2个单位长度的速度沿数轴向右匀速运动,设运动时间为 x ( x 大于0)秒.![]()
(1)点C表示的数是;
(2)当 ![]() 秒时,点P到达点A处?
秒时,点P到达点A处?
(3)运动过程中点P表示的数是(用含字母 ![]() 的式子表示);
的式子表示);
(4)当P,C之间的距离为2个单位长度时,求 x 的值.
参考答案:
【答案】
(1)1
(2)5
(3)![]() ?4+2x
?4+2x
(4)解:①当点P在点C左边时,
∵P、C之间的距离为2个单位长度,
∴点P表示的数为-1,
∴2x-4=-1,
∴x=![]() .
.
②当点P在点C右边时,
∵P、C之间的距离为2个单位长度,
∴点P表示的数为3,
∴2x-4=3,
∴x=![]() .
.
综上所述:当x=![]() 或
或![]() 时,P,C之间的距离为2个单位长度.
时,P,C之间的距离为2个单位长度.
【解析】解:(1)∵点C到点A、点B的距离相等,
∴C为AB的中点,
∴点C表示的数为:![]() =1.
=1.
所以答案是:1.
(2)依题可得:
AB=6-(-4)=10,
∴10÷2=5(秒).
答:但x为5秒时,点P到达点A处.
(3)依题可得:
运动过程中点P表示的数为:-4+2x.
所以答案是:2x-4.
【考点精析】本题主要考查了数轴的相关知识点,需要掌握数轴是规定了原点、正方向、单位长度的一条直线才能正确解答此题.
-
科目: 来源: 题型:
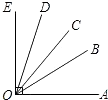
查看答案和解析>>【题目】如图所示,∠AOE=90°,∠BOD=45°,那么图中不大于90°的角有个,它们的度数之和是°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】用正方形使纸板做三棱柱盒子,每个盒子由3个长方形侧面和2个正三角形底面组成.硬纸板以如图两种方法裁剪(裁剪后边角料不再利用)). A方法:剪6个侧面;
B方法:剪4个侧面和5个底面.
现有19张硬纸板,裁剪时x张用A方法,其余用B方法.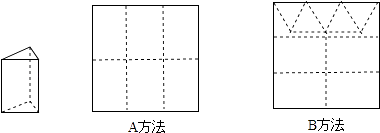
(1)分别求裁剪出的侧面和底面的个数(用x的代数式表示)
(2)若裁剪出的侧面和底面恰好全部用完,问能做多少个盒子? -
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,ABCD中,E、F分别是边AB、CD的中点.
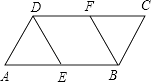
(1)求证:四边形EBFD是平行四边形;
(2)若AD=AE=2,∠A=60°,求四边形EBFD的周长. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠ACB=90°,AC=BC , BE⊥CE于点E . AD⊥CE于点D.求证:△BEC≌△CDA.
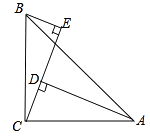
-
科目: 来源: 题型:
查看答案和解析>>【题目】据统计2018年我国国民总产值为900309亿元,比上年增长了6.6%,首次突破90万亿,则900309亿元用科学记数法可表示为( )元.
A.9.003 09×1012B.0.900 309×1012
C.9.003 09×1013D.0.900 309×1014
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠B=90°,BC=5
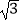 ,∠C=30°.点D从点C出发沿CA方向以每秒2个单位长的速度向A点匀速运动,同时点E从点A出发沿AB方向以每秒1个单位长的速度向点B匀速运动,当其中一个点到达终点时,另一个点也随之停止运动.设点D、E运动的时间是t秒(t>0).过点D作DF⊥BC于点F,连接DE、EF.
,∠C=30°.点D从点C出发沿CA方向以每秒2个单位长的速度向A点匀速运动,同时点E从点A出发沿AB方向以每秒1个单位长的速度向点B匀速运动,当其中一个点到达终点时,另一个点也随之停止运动.设点D、E运动的时间是t秒(t>0).过点D作DF⊥BC于点F,连接DE、EF.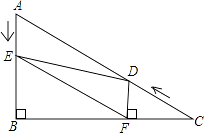
(1)AC的长是 , AB的长是 .
(2)在D、E的运动过程中,线段EF与AD的关系是否发生变化?若不变化,那么线段EF与AD是何关系,并给予证明;若变化,请说明理由.
(3)四边形AEFD能够成为菱形吗?如果能,求出相应的t值;如果不能,说明理由.
(4)当t为何值,△BEF的面积是2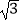 ?
?
相关试题

