【题目】某商场试销一种商品,成本为每件200元,规定试销期间销售单价不低于成本单价,且获利不得高于50%,一段时间后,发现销售量y(件)与销售单价x(元)之间的函数关系如下表:
销售单价x(元) | … | 230 | 235 | 240 | 245 | … |
销售量y(件) | … | 440 | 430 | 420 | 410 | … |
(1)请根据表格中所给数据,求出y关于x的函数关系式;
(2)设商场所获利润为w元,将商品销售单价定为多少时,才能使所获利润最大?最大利润是多少?
参考答案:
【答案】(1)y与x的函数关系式为y=﹣2x+900;
(2)商品的销售单价定为300元时,才能使所获利润最大,最大利润时30000元.
【解析】
试题分析:(1)设y与x的函数关系式为y=kx+b,利用待定系数法求得函数的解析式即可;
(2)先求得单价的定价范围,然后根据利润=每件获利×件数列出利润的函数关系式,然后根据自变量的取值和二次函数的对称性即可求得最大利润.
解:(1)根据所给数据可知y与x的图象是一条直线.设y与x的函数关系式为y=kx+b.
将x=230,y=440;x=235,y=430代入y=kx+b得:![]() ,解得:
,解得:![]()
∴y=﹣2x+900
经验证,x=240,y=420;x=245,y=410都满足上述函数关系式
∴y与x的函数关系式为y=﹣2x+900;
(2)由题意得:200≤x≤200×(1+50%),
∴200≤x≤300.
W=(x﹣200)(﹣2x+900)=﹣2(x﹣325)2+31250
∵a=﹣2<0,
∴抛物线开口向下.
∵200≤x≤300,在对称轴x=325的左侧,
∴W随x的增大而增大.
∴当x=300时,W有最大值,W最大=﹣2×(300﹣325)2+31250=30000元.
答:商品的销售单价定为300元时,才能使所获利润最大,最大利润时30000元.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知一组数据a1,a2,a3,a4,a5的平均数为8,则另一组数据a1+10,a2﹣10,a3+10,a4﹣10,a5+10的平均数为( )
A. 6 B. 8 C. 10 D. 12
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠ABC=90°,AB=BC=
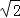 ,将△ABC绕点C逆时针旋转60°,得到△MNC,连接BM,则BM的长是 .
,将△ABC绕点C逆时针旋转60°,得到△MNC,连接BM,则BM的长是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,抛物线与x轴交于点A(﹣1,0)和点B(1,0),直线y=2x﹣1与y轴交于点C,与抛物线交于点C、D.
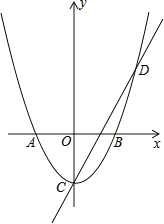
(1)求抛物线的解析式;
(2)求点A到直线CD的距离;
(3)平移抛物线,使抛物线的顶点P在直线CD上,抛物线与直线CD的另一个交点为Q,点G在y轴正半轴上,当以G、P、Q三点为顶点的三角形为等腰直角三角形时,求出所有符合条件的G点的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,E是正方形ABCD申CD边上任意一点.
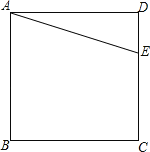
(1)以点A为中心,把△ADE顺时针旋转90°,画出旋转后的图形;
(2)在BC边上画一点F,使△CFE的周长等于正方形ABCD的周长的一半,请简要说明你取该点的理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】把下列各数填入它所属的集合内:
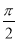 ,0,5.2,
,0,5.2, 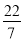 ,+(﹣4),﹣2
,+(﹣4),﹣2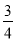 ,﹣(﹣3 ),0.25555…,﹣0.030030003…
,﹣(﹣3 ),0.25555…,﹣0.030030003…(1)分数集合:{______ …}
(2)非负整数集合:{______ …}
(3)有理数集合:{______ …}.
-
科目: 来源: 题型:
查看答案和解析>>【题目】将抛物线y=ax2向右平移2个单位,再向上平移3个单位,移动后的抛物线经过点(3,﹣1),那么移动后的抛物线的关系式为 .
相关试题

