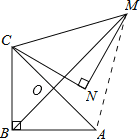
【题目】如图,在Rt△ABC中,∠ABC=90°,AB=BC=![]() ,将△ABC绕点C逆时针旋转60°,得到△MNC,连接BM,则BM的长是 .
,将△ABC绕点C逆时针旋转60°,得到△MNC,连接BM,则BM的长是 .

参考答案:
【答案】1+![]() .
.
【解析】
试题分析:如图,连接AM,由题意得:CA=CM,∠ACM=60°,得到△ACM为等边三角形根据AB=BC,CM=AM,得出BM垂直平分AC,于是求出BO=![]() AC=1,OM=CMsin60°=
AC=1,OM=CMsin60°=![]() ,最终得到答案BM=BO+OM=1+
,最终得到答案BM=BO+OM=1+![]() .
.
解:如图,连接AM,
由题意得:CA=CM,∠ACM=60°,
∴△ACM为等边三角形,
∴AM=CM,∠MAC=∠MCA=∠AMC=60°;
∵∠ABC=90°,AB=BC=![]() ,
,
∴AC=2=CM=2,
∵AB=BC,CM=AM,
∴BM垂直平分AC,
∴BO=![]() AC=1,OM=CMsin60°=
AC=1,OM=CMsin60°=![]() ,
,
∴BM=BO+OM=1+![]() ,
,
故答案为:1+![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,点(﹣2,3)所在的象限是( )
A. 第一象限 B. 第二象限 C. 第三象限 D. 第四象限
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列运算正确的是( )
A. -3-2=-1 B. -32=8 C. 2xy+xy=3xy D. 2x+x2=3x2
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知一组数据a1,a2,a3,a4,a5的平均数为8,则另一组数据a1+10,a2﹣10,a3+10,a4﹣10,a5+10的平均数为( )
A. 6 B. 8 C. 10 D. 12
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,抛物线与x轴交于点A(﹣1,0)和点B(1,0),直线y=2x﹣1与y轴交于点C,与抛物线交于点C、D.
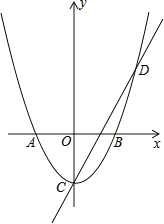
(1)求抛物线的解析式;
(2)求点A到直线CD的距离;
(3)平移抛物线,使抛物线的顶点P在直线CD上,抛物线与直线CD的另一个交点为Q,点G在y轴正半轴上,当以G、P、Q三点为顶点的三角形为等腰直角三角形时,求出所有符合条件的G点的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某商场试销一种商品,成本为每件200元,规定试销期间销售单价不低于成本单价,且获利不得高于50%,一段时间后,发现销售量y(件)与销售单价x(元)之间的函数关系如下表:
销售单价x(元)
…
230
235
240
245
…
销售量y(件)
…
440
430
420
410
…
(1)请根据表格中所给数据,求出y关于x的函数关系式;
(2)设商场所获利润为w元,将商品销售单价定为多少时,才能使所获利润最大?最大利润是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,E是正方形ABCD申CD边上任意一点.
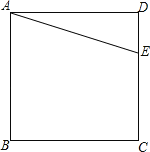
(1)以点A为中心,把△ADE顺时针旋转90°,画出旋转后的图形;
(2)在BC边上画一点F,使△CFE的周长等于正方形ABCD的周长的一半,请简要说明你取该点的理由.
相关试题

