【题目】若![]() 的度数是
的度数是![]() 的度数的k倍,则规定
的度数的k倍,则规定![]() 是
是![]() 的k倍角.
的k倍角.
(1)若∠M=21°17',则∠M的5倍角的度数为 ;
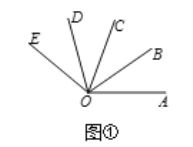
(2)如图1,OB是∠AOC的平分线,OD是∠COE的平分线,若∠AOC=∠COE,请直接写出图中∠AOB的所有3倍角;
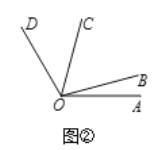
(3)如图2,若∠AOC是∠AOB的5倍角,∠COD是∠AOB的3倍角,且∠AOC和∠BOD互为补角,求∠AOD的度数.
参考答案:
【答案】(1)106°25';(2)∠AOD,∠BOE;(3)120°.
【解析】
(1)根据题意,列式计算即可得到答案;
(2)由角平分线性质定理,结合∠AOC=∠COE,得到∠AOB=∠BOC=∠COD=∠DOE,即可得到∠AOD=3∠AOB,∠BOE=3∠AOB;
(3)设∠AOB=x,则∠AOC=5x,∠BOC=4x,∠COD=3x,则利用∠AOC和∠BOD互为补角的关系,列出方程,即可得到x的值,然后得到答案.
解:(1)![]() ;
;
故答案为:![]() .
.
(2)∵OB是∠AOC的平分线,OD是∠COE的平分线,∠AOC=∠COE,
∴∠AOB=∠BOC=∠COD=∠DOE,
∴∠AOD=3∠AOB,∠BOE=3∠AOB;
∴图中∠AOB的所有3倍角有:∠AOD,∠BOE;
(3)设∠AOB=x,则∠AOC=5x,∠COD=3x.
∴∠BOC=4x,
∵∠AOC和∠BOD互为补角,
∴∠AOC+∠BOD=∠AOC+∠BOC+∠COD=180°,
即5x+7x=180°,
解得:x=15°.
∴∠AOD=8x=120°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某公交公司决定更换节能环保的新型公交车,购买的数量和所需费用如下表所示:
(1)求A型和B型公交车的单价:
(2)该公司计划购买A型和B型两种公交车共10辆,已知每辆A型公交车年均载客量为60万人次,每辆B型公交车年均载客量为100万人次;公交公司该如何购买这10辆公交车,才能确保公交车的年均载客量的总和不少于670万人次,且所需费用最省,并求出最省的费用

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:平行四边形ABCD的对角线AC,BD相交于点O.
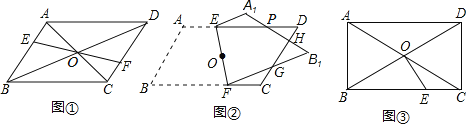
(1)如图①,EF过点O且与AB,CD分别相交于点E、F,AC=6,△AEO的周长为10,求CF+OF的值.
(2)如图②,将平行四边形ABCD(纸片)沿过对角线交点O的直线EF折叠,点A落在A1处,点B落在点B1处,设FB1交CD于点G,A1B1分别交CD、DE于点H、P,请在折叠后的图形中找一条线段,使它与EP相等,并加以证明.
(3)如图③,△ABO是等边三角形,AB=1,点E在BC边上,且BE=1,则2EC-2EO= 直接填结果.
-
科目: 来源: 题型:
查看答案和解析>>【题目】希腊数学家丢番图(公元3-4世纪)的墓碑上记载着: “他生命的六分之一是幸福的童年;再活了他生命的十二分之一,两颊长起了细细的胡须;他结了婚,又度过了一生的七分之一;再过五年,他有了儿子,感到很幸福;可是儿子只活了他父亲全部年龄的一半;儿子死后,他在极度悲痛中度过了四年,也与世长辞了.”
根据以上信息,请你算出:
(1)丢番图的寿命;
(2)丢番图开始当爸爸时的年龄;
(3)儿子死时丢番图的年龄.
-
科目: 来源: 题型:
查看答案和解析>>【题目】定义:若关于x的一元二次方程ax2+bx+c=0(a≠0)的两个实数根为x1,x2(x1<x2),分别以x1,x2为横坐标和纵坐标得到点M(x1,x2),则称点M为该一元二次方程的衍生点.
(1)若方程为x2-2x=0,写出该方程的衍生点M的坐标.
(2)若关于x的一元二次方程x2-(2m+1)x+2m=0(m<0)的衍生点为M,过点M向x轴和y轴作垂线,两条垂线与坐标轴恰好围成一个正方形,求m的值.
(3)是否存在b,c,使得不论k(k≠0)为何值,关于x的方程x2+bx+c=0的衍生点M始终在直线y=kx-2(k-2)的图象上,若有请直接写出b,c的值,若没有说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】点A,B在数轴上表示的数如图所示. 动点P从点A出发,沿数轴向右以每秒2个单位长度的速度运动到点B,再从点B以同样的速度运动到点A停止,设点P运动的时间为t秒,解答下列问题.

(1)当t=2时,AP= 个单位长度,当t=6时,AP= 个单位长度;
(2)直接写出整个运动过程中AP的长度(用含t的代数式表示);
(3)当AP=6个单位长度时,求t的值;
(4)当点P运动到线段AB的3等分点时,t的值为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示的一块地,∠ADC=90°,AD=4m,CD=3m,AB=13m,BC=12m,求这块地的面积.

相关试题

