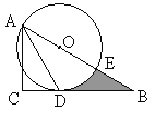
【题目】如图,在Rt△ABC中,∠C=90°,∠BAC的平分线AD交BC边于点D.以AB上一点O为圆心作⊙O,使⊙O经过点A和点D.
(1)判断直线BC与⊙O的位置关系,并说明理由;
(2)若AC=3,∠B=30°,设⊙O与AB边的另一个交点为E,求线段BD,BE与劣弧![]() 所围成的阴影部分的面积(结果保留根号和
所围成的阴影部分的面积(结果保留根号和![]() )。
)。
参考答案:
【答案】(1)直线BC是⊙O的切线;(2)2![]() -
-![]()
【解析】
(1) 连接OD, 根据平行线判定推出OD//AC, 推出OD⊥BC, 根据切线的判定推出即可;
(2) 根据含有30角的直角三角形的性质得出OB=2OD=2r, AB=2AC=3r, 从而求得半径r的
值,根据S阴影=SΔODB-SΔODE求出答案即可.
(1)解:连接OD 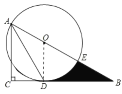
∵OA=OD ∴∠OAD=∠ODA
又AD平分∠BAC
∵∠OAD=∠CAD
∴∠ODA=∠CAD ∴AC∥OD
又∠C=90° ∴OD⊥BC
又点D在⊙O上
∴直线BC是⊙O的切线
(2)在RtΔACB中,∠B=30°∴AB=2AC=6
设⊙O半径为r,则OD=r,OA=r,OB=AB-OA=6-r
在RtΔODB中,∠B=30°∴OB=2OD ∴6-r=r
得r=2,BD=2![]() ,∠BOD=60°
,∠BOD=60°
S阴影=SΔODB-SΔODE=2![]() -
-![]()
-
科目: 来源: 题型:
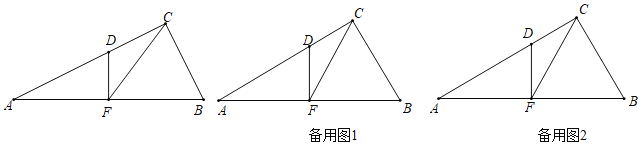
查看答案和解析>>【题目】如图,在Rt△ABC中,∠ACB=90°,∠A=30°,AB=12,点F是AB的中点,过点F作FD⊥AB交AC于点D.
(1)若△AFD以每秒2个单位长度的速度沿射线FB向右移动,得到△A1F1D1,当F1与点B重合时停止移动.设移动时间为t秒,△A1F1D1与△CBF重叠部分的面积记为S.直接写出S与t的函数关系式.
(2)在(1)的基础上,如果D1,B,F构成的△D1BF为等腰三角形,求出t值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=1,且经过点(﹣1,0),下列四个结论:①如果点(
 ,y1)和(2,y2)都在抛物线上,那么y1<y2;②b2﹣4ac>0;③m(am+b)<a+b(m≠1的实数);④
,y1)和(2,y2)都在抛物线上,那么y1<y2;②b2﹣4ac>0;③m(am+b)<a+b(m≠1的实数);④ ;其中正确的有( )
;其中正确的有( )
A. 4个 B. 3个 C. 2个 D. 1个
-
科目: 来源: 题型:
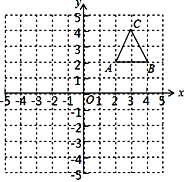
查看答案和解析>>【题目】如图,在平面直角坐标系中,△ABC的三个顶点都在格点上,点A的坐标为(2,2)请解答下列问题:
(1)画出△ABC关于原点O成中心对称的△A1B1C1,并写出A1的坐标;
(2)画出△ABC绕点B逆时针旋转90°后得到的△A2B2C2,并求出点C在旋转过程中经过的路径长是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,锐角
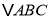 中,
中,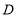 ,
,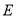 分别是
分别是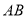 ,
,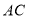 边上的点,
边上的点,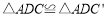 ,
,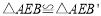 ,且
,且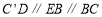 ,
, 、
、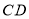 交于点
交于点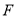 ,若
,若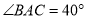 ,则
,则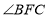 的大小是( )
的大小是( )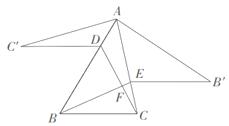
A.
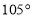 B.
B.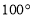 C.
C.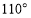 D.
D.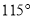
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图(1),在
 和
和 中,
中, 为
为 边
边 上一点,
上一点, 平分
平分 ,
,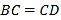 ,
, .
. 
(1)求证:

(2)如图(2),若
 ,连接
,连接 交
交 于
于 ,
, 为边
为边 上一点,满足
上一点,满足 ,连接
,连接 交
交 于
于 . ①求
. ①求 的度数;
的度数; ②若
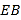 平分
平分 ,试说明:
,试说明: 平分
平分 .
. -
科目: 来源: 题型:
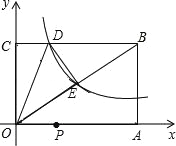
查看答案和解析>>【题目】如图,已知矩形OABC的两边OA、OC分别落在x轴、y轴的正半轴上,顶点B的坐标是(6,4),反比例函数y=
 (x>0)的图象经过矩形对角线的交点E,且与BC边交于点D.
(x>0)的图象经过矩形对角线的交点E,且与BC边交于点D.(1)①求反比例函数的解析式与点D的坐标;②直接写出△ODE的面积;
(2)若P是OA上的动点,求使得“PD+PE之和最小”时的直线PE的解析式.
相关试题

