【题目】【试题背景】已知:l ∥m∥n∥k,平行线l与m、m与n、n与k之间的距离分别为d1、d2、d3 , 且d1 =d3 = 1,d2 = 2 .我们把四个顶点分别在l、m、n、k这四条平行线上的四边形称为“格线四边形”.
(1)【探究1】如图1,正方形ABCD为“格线四边形”,BE![]() L于点E,BE的反向延长线交直线k于点F. 求正方形ABCD的边长.
L于点E,BE的反向延长线交直线k于点F. 求正方形ABCD的边长.
(2)【探究2】矩形ABCD为“格线四边形”,其长 :宽 = 2 :1 ,求矩形ABCD的宽
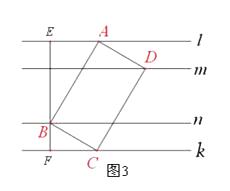
(3)【探究3】如图2,菱形ABCD为“格线四边形”且∠ADC=60°,△AEF是等边三角形, ![]() 于点E, ∠AFD=90°,直线DF分别交直线l、k于点G、M. 求证:EC=DF.
于点E, ∠AFD=90°,直线DF分别交直线l、k于点G、M. 求证:EC=DF.
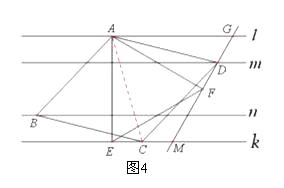
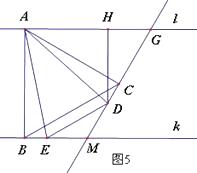
(4)【拓 展】如图3,l ∥k,等边三角形ABC的顶点A、B分别落在直线l、k上, ![]() 于点B,且AB=4 ,∠ACD=90°,直线CD分别交直线l、k于点G、M,点D、E分别是线段GM、BM上的动点,且始终保持AD=AE,
于点B,且AB=4 ,∠ACD=90°,直线CD分别交直线l、k于点G、M,点D、E分别是线段GM、BM上的动点,且始终保持AD=AE, ![]() 于点H.
于点H.
猜想:DH在什么范围内,BC∥DE?直接写出结论。
参考答案:
【答案】
(1)解:如图1,
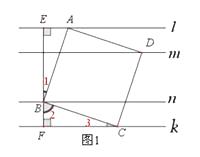
∵BE⊥l , l ∥k ,
∴∠AEB=∠BFC=90°, 又四边形ABCD是正方形,
∴∠1+∠2=90°,AB=BC,
∵∠2+∠3=90°,
∴ ∠1=∠3,∴⊿ABE≌⊿BCF(AAS),
∴AE=BF=1 ,
∵BE=d1+d2=3 ,
∴AB= ![]() =
= ![]() ,
,
∴正方形的边长是 ![]()
(2)解:(注意:要分2种情况讨论)如图2,3
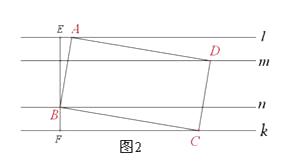
∵ ⊿ABE∽⊿BCF,
∴ ![]() 或
或 ![]() ,
,
∵BF=d3=1 ,
∴AE= ![]() 或AE=2,
或AE=2,
∴AB= ![]() =
= ![]() 或 AB=
或 AB= ![]() =
= ![]() ,
,
∴矩形ABCD的宽为 ![]() 或
或 ![]()
(3)解:如图4,连接AC,
∵四边形ABCD是菱形,
∴AD=DC,又∠ADC=60°,
∴⊿ADC是等边三角形,
∴AD=AC,
∵AE⊥k , ∠AFD=90°,
∴∠AEC=∠AFD=90°,
∵⊿AEF是等边三角形,
∴ AF=AE,
∴⊿AFD≌⊿AEC(HL),
∴EC=DF
(4)解:如图5,当2<DH<4时, BC∥DE .
【解析】(1)根据垂线的定义及平行线的性质得出∠AEB=∠BFC=90°,根据正方形的性质得出∠1+∠2=90°,AB=BC, 然后利用同角的余角相等得出 ∠1=∠3,利用AAS证明△ABE≌△BCF,根据全等三角形的性质得出AE和BE的长,然后利用勾股定理即可求解;
(2) 过B作BE⊥l于点E,交k于点F,易证△AEB∽△BCF,然后根据相似三角形对应边成比例,得出![]() =
=![]() =
=![]() 或
或![]() =
=![]() =
=![]() 又BF=d3=1 , 故AE=
又BF=d3=1 , 故AE= ![]() 或AE=2,然后分AB是长和AB是宽两种情况进行讨论求得;
或AE=2,然后分AB是长和AB是宽两种情况进行讨论求得;
(3)连接AC,根据菱形的性质知AD=DC,又∠ADC=60°,进而判断出△ADC是等边三角形,根据等边三角形的性质得出AD=AC,AF=AE,根据垂直的定义得出∠AEC=∠AFD=90°,再证明△AFD≌△AEC(HL),根据全等三角形的对应边相等即可证得;
(4)连接AM,首先证明△ABE≌△ACD,然后证明Rt△ABM≌Rt△ACM(HL),根据全等三角形的对应角相等,以及等腰直角三角形 的性质证明∠MBC=∠MED,则ED∥BC即可证得.
【考点精析】通过灵活运用菱形的性质和矩形的性质,掌握菱形的四条边都相等;菱形的对角线互相垂直,并且每一条对角线平分一组对角;菱形被两条对角线分成四个全等的直角三角形;菱形的面积等于两条对角线长的积的一半;矩形的四个角都是直角,矩形的对角线相等即可以解答此题.
-
科目: 来源: 题型:
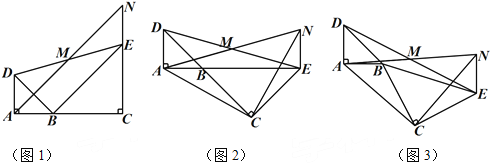
查看答案和解析>>【题目】如图1,已知△BAD和△BCE均为等腰直角三角形,∠BAD=∠BCE=90°,点M为DE的中点.过点E与AD平行的直线交射线AM于点N.
(1)当A,B,C三点在同一直线上时(如图1),求证:M为AN的中点;
(2)将图1中△BCE绕点B旋转,当A,B,E三点在同一直线上时(如图2),求证:△CAN为等腰直角三角形;
(3)将图1中△BCE绕点B旋转到图3的位置时,(2)中的结论是否仍然成立?若成立,试证明之;若不成立,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知AC平分∠BAD,CE⊥AB于E,CF⊥AD于F,且BC=CD.
(1)求证:△BCE≌△DCF;
(2)求证:AB+AD=2AE.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=AC,∠BAC=50°,∠BAC的平分线与AB的中垂线交于点O,点C沿EF折叠后与点O重合,则∠CEO的度数是_____.

-
科目: 来源: 题型:
查看答案和解析>>【题目】若一个两位正整数m的个位数为8,则称m为“好数”.
(1)求证:对任意“好数”m,m2-64一定为20的倍数;
(2)若m=p2-q2,且p,q为正整数,则称数对(p,q)为“友好数对”,规定:
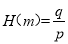 ,例如68=182-162,称数对(18,16)为“友好数对”,则
,例如68=182-162,称数对(18,16)为“友好数对”,则 ,求小于50的“好数”中,所有“友好数对”的H(m)的最大值.
,求小于50的“好数”中,所有“友好数对”的H(m)的最大值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,某市有一块长为(3a+b)米,宽为(2a+b)米的长方形地块,中间是边长为(a+b)米的正方形,规划部门计划将在中间的正方形修建一座雕像,四周的阴影部分进行绿化,
(1)绿化的面积是多少平方米?(用含字母a、b的式子表示)
(2)求出当a=20,b=12时的绿化面积.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC的外角∠ACD的平分线CP与内角∠ABC平分线BP交于点P,若∠BPC=40°,求∠CAB和∠CAP的度数.

相关试题

