【题目】探究与发现:
探究一:我们知道,三角形的一个外角等于与它不相邻的两个内角的和.那么,三角形的一个内角与它不相邻的两个外角的和之间存在何种数量关系呢?
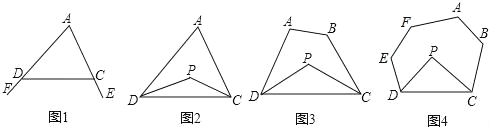
已知:如图1,∠FDC与∠ECD分别为△ADC的两个外角,试探究∠A与∠FDC+∠ECD的数量关系.
探究二:三角形的一个内角与另两个内角的平分线所夹的钝角之间有何种关系?
已知:如图2,在△ADC中,DP、CP分别平分∠ADC和∠ACD,试探究∠P与∠A的数量关系.
探究三:若将△ADC改为任意四边形ABCD呢?
已知:如图3,在四边形ABCD中,DP、CP分别平分∠ADC和∠BCD,试利用上述结论探究∠P与∠A+∠B的数量关系.
探究四:若将上题中的四边形ABCD改为六边形ABCDEF(图4)呢?
请直接写出∠P与∠A+∠B+∠E+∠F的数量关系: .
参考答案:
【答案】探究一:∠FDC+∠ECD =180°+∠A;探究二:∠DPC=90°+![]() ∠A;探究三:∠PDC==
∠A;探究三:∠PDC==![]() (∠A+∠B);探究四:∠P=
(∠A+∠B);探究四:∠P=![]() (∠A+∠B+∠E+∠F)﹣180°
(∠A+∠B+∠E+∠F)﹣180°
【解析】试题分析:探究一:根据三角形的一个外角等于与它不相邻的两个内角的和可得∠FDC=∠A+∠ACD,∠ECD=∠A+∠ADC,再根据三角形内角和定理整理即可得解;
探究二:根据角平分线的定义可得∠PDC=![]() ∠ADC,∠PCD=
∠ADC,∠PCD=![]() ∠ACD,然后根据三角形内角和定理列式整理即可得解;
∠ACD,然后根据三角形内角和定理列式整理即可得解;
探究三:根据四边形的内角和定理表示出∠ADC+∠BCD,然后同理探究二解答即可;
探究四:根据六边形的内角和公式表示出∠ADC+∠BCD,然后同理探究二解答即可.
解:探究一:∵∠FDC=∠A+∠ACD,∠ECD=∠A+∠ADC,
∴∠FDC+∠ECD=∠A+∠ACD+∠A+∠ADC=180°+∠A;
探究二:∵DP、CP分别平分∠ADC和∠ACD,
∴∠PDC=![]() ∠ADC,∠PCD=
∠ADC,∠PCD=![]() ∠ACD,
∠ACD,
∴∠DPC=180°﹣∠PDC﹣∠PCD,
=180°﹣![]() ∠ADC﹣
∠ADC﹣![]() ∠ACD,
∠ACD,
=180°﹣![]() (∠ADC+∠ACD),
(∠ADC+∠ACD),
=180°﹣![]() (180°﹣∠A),
(180°﹣∠A),
=90°+![]() ∠A;
∠A;
探究三:∵DP、CP分别平分∠ADC和∠BCD,
∴∠PDC=![]() ∠ADC,∠PCD=
∠ADC,∠PCD=![]() ∠BCD,
∠BCD,
∴∠DPC=180°﹣∠PDC﹣∠PCD,
=180°﹣![]() ∠ADC﹣
∠ADC﹣![]() ∠BCD,
∠BCD,
=180°﹣![]() (∠ADC+∠BCD),
(∠ADC+∠BCD),
=180°﹣![]() (360°﹣∠A﹣∠B),
(360°﹣∠A﹣∠B),
=![]() (∠A+∠B);
(∠A+∠B);
探究四:六边形ABCDEF的内角和为:(6﹣2)180°=720°,
∵DP、CP分别平分∠EDC和∠BCD,
∴∠P=![]() ∠ADC,∠PCD=
∠ADC,∠PCD=![]() ∠ACD,
∠ACD,
=180°﹣![]() ∠ADC﹣
∠ADC﹣![]() ∠ACD,
∠ACD,
=180°﹣![]() (∠ADC+∠ACD),
(∠ADC+∠ACD),
=180°﹣![]() (720°﹣∠A﹣∠B﹣∠E﹣∠F),
(720°﹣∠A﹣∠B﹣∠E﹣∠F),
=![]() (∠A+∠B+∠E+∠F)﹣180°,
(∠A+∠B+∠E+∠F)﹣180°,
即∠P=![]() (∠A+∠B+∠E+∠F)﹣180°.
(∠A+∠B+∠E+∠F)﹣180°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线y=x﹣1与反比例函数y=
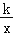 的图象交于A、B两点,与x轴交于点C,已知点A的坐标为(﹣1,m).
的图象交于A、B两点,与x轴交于点C,已知点A的坐标为(﹣1,m).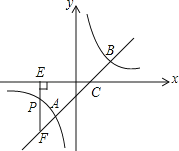
(1)求反比例函数的解析式;
(2)若点P(n,﹣1)是反比例函数图象上一点,过点P作PE⊥x轴于点E,延长EP交直线AB于点F,求△CEF的面积.
(3)在x轴上是否存在点Q,使得△QBC是等腰三角形?若存在,请直接写出Q点坐标;若不存在,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,台球运动中,如果母球P击中边点A,经桌边反弹后击中相邻的另一桌边的点B,两次反弹.
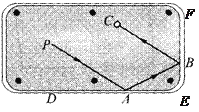
(1)若∠PAD=32度,求∠PAB的度数;
(2)母球P经过的路线BC与PA一定平行吗?请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在矩形ABCD中,AB=8,BC=12,点E是BC的中点,连接AE,将△ABE沿AE折叠,点B落在点F处,连接FC,则tan∠ECF=( )
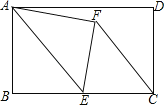
A.
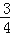 B.
B.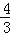 C.
C.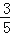 D.
D.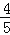
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,已知△ABC的三个顶点的坐标分别为A(﹣2,3),B(﹣6,0),C(﹣1,0).

(1)请直接写出点B关于点A对称的点的坐标;
(2)将△ABC绕坐标原点O逆时针旋转90°,画出图形,直接写出点B的对应点的坐标;
(3)请直接写出:以A、B、C为顶点的平行四边形的第四个顶点D的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若3a+2b-1>2a+3b,则a、b的大小关系为( )
A. a<b B. a>b C. a=b D. 不能确定
-
科目: 来源: 题型:
查看答案和解析>>【题目】陕西省元月份某一天的天气预报中,延安市的最低气温为﹣6℃,西安市的最低气温为2℃,这一天延安市的最低气温比西安市的最低气温低( )
A.8℃
B.﹣8℃
C.6℃
D.2℃
相关试题

