【题目】在Rt△ABC和Rt△DEF中,∠C=∠F=90°,下列条件不能判定Rt△ABC≌Rt△DEF的是( )
A. AC=DF,∠B=∠EB. ∠A=∠D,∠B=∠E
C. AB=DE,AC=DFD. AB=DE,∠A=∠D
参考答案:
【答案】B
【解析】
本题主要考查两个三角形全等的条件:两边夹一角(SAS),两角夹一边(ASA),两角对一边(AAS),三条边(SSS),HL.且要明确满足下列条件之一的两个三角形是全等的:
(1)有两边和第三边上的中线对应相等;
(2)有两边和第三边上的高对应相等;
(3)有两边和第三边上的角平分线对应相等;
解:A、∵在Rt△ABC和Rt△DEF中
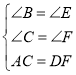
∴Rt△ABC≌Rt△DEF(AAS),故本选项不符合题意;
B、在Rt△ABC和Rt△DEF中,根据∠A=∠D、∠C=∠F\、∠B=∠E不能推出两三角形全等,故本选项符合题意;
C、∵在Rt△ABC和Rt△DEF中
![]()
∴Rt△ABC≌Rt△DEF(HL),故本选项不符合题意;
D、∵在Rt△ABC和Rt△DEF中

∴Rt△ABC≌Rt△DEF(AAS),故本选项不符合题意;
故选:B.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在直角梯形ABCD中,AD∥BC,∠D=∠C=90°,点E在DC上,且AE,BE分别平分∠BAD和∠ABC.
(1)求证:点E为CD中点;
(2)当AD=2,BC=3时,求AB的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】请你认真阅读下面的小探究系列,完成所提出的问题.
(1)如图1,将角尺放在正方形ABCD上,使角尺的直角顶点E与正方形ABCD的顶点D重合,角尺的一边交CB于点F,将另一边交BA的延长线于点G.求证:EF=EG.
(2)如图2,移动角尺,使角尺的顶点E始终在正方形ABCD的对角线BD上,其余条件不变,请你思考后直接回答EF和EG的数量关系:EF EG(用“=”或“≠”填空)
(3)运用(1)(2)解答中所积累的活动经验和数学知识,完成下题:如图3,将(2)中的“正方形ABCD”改成“矩形ABCD”,使角尺的一边经过点A(即点G、A重合),其余条件不变,若AB=4,BC=3,求
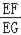 的值.
的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】2018年5月3日,中国科学院在上海发布了中国首款人工智能芯片:寒武纪(MLU100),该芯片在平衡模式下的等效理论峰值速度达每秒128 000 000 000 000次定点运算,将数
128 000 000 000 000用科学计数法表示为( )
A. 1.28
 1014 B. 1.28
1014 B. 1.28 10-14 C. 128
10-14 C. 128 1012 D. 0.128
1012 D. 0.128 1011
1011 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AE是中线,AD是角平分线,AF是高,填空:
(1)BE= =
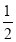
(2)∠BAD=
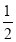
(3)∠AFB= =90°
(4)S△ABC= S△ABE.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在正方形ABCD中,AB=3,点M在CD的边上,且DM=1,ΔAEM与ΔADM关于AM所在的直线对称,将ΔADM按顺时针方向绕点A旋转90°得到ΔABF,连接EF,则线段EF的长为( )
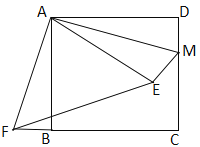
A. 3 B.
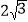 C.
C. 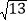 D.
D. 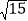
-
科目: 来源: 题型:
查看答案和解析>>【题目】有
 筐白菜,以每筐
筐白菜,以每筐 千克为标准,超过或不足的分别用正、负来表示,记录如下:
千克为标准,超过或不足的分别用正、负来表示,记录如下:与标准质量的差
 单位:千克
单位:千克






筐 数






(1)与标准质量比较,
 筐白菜总计超过或不足多少千克?
筐白菜总计超过或不足多少千克?(2)若白菜每千克售价
 元,则出售这
元,则出售这 筐白菜可卖多少元?
筐白菜可卖多少元?
相关试题

