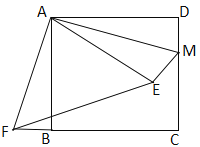
【题目】如图,在正方形ABCD中,AB=3,点M在CD的边上,且DM=1,ΔAEM与ΔADM关于AM所在的直线对称,将ΔADM按顺时针方向绕点A旋转90°得到ΔABF,连接EF,则线段EF的长为( )
A. 3 B. ![]() C.
C. ![]() D.
D. ![]()
参考答案:
【答案】C
【解析】连接BM.证明△AFE≌△AMB得FE=MB,再运用勾股定理求出BM的长即可.
连接BM,如图,
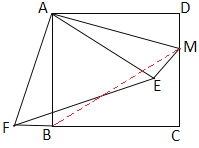
由旋转的性质得:AM=AF.
∵四边形ABCD是正方形,
∴AD=AB=BC=CD,∠BAD=∠C=90°,
∵ΔAEM与ΔADM关于AM所在的直线对称,
∴∠DAM=∠EAM.
∵∠DAM+∠BAM=∠FAE+∠EAM=90°,
∴∠BAM=∠EAF,
∴△AFE≌△AMB
∴FE=BM.
在Rt△BCM中,BC=3,CM=CD-DM=3-1=2,
∴BM=![]()
∴FE=![]() .
.
故选C.
-
科目: 来源: 题型:
查看答案和解析>>【题目】2018年5月3日,中国科学院在上海发布了中国首款人工智能芯片:寒武纪(MLU100),该芯片在平衡模式下的等效理论峰值速度达每秒128 000 000 000 000次定点运算,将数
128 000 000 000 000用科学计数法表示为( )
A. 1.28
 1014 B. 1.28
1014 B. 1.28 10-14 C. 128
10-14 C. 128 1012 D. 0.128
1012 D. 0.128 1011
1011 -
科目: 来源: 题型:
查看答案和解析>>【题目】在Rt△ABC和Rt△DEF中,∠C=∠F=90°,下列条件不能判定Rt△ABC≌Rt△DEF的是( )
A. AC=DF,∠B=∠EB. ∠A=∠D,∠B=∠E
C. AB=DE,AC=DFD. AB=DE,∠A=∠D
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AE是中线,AD是角平分线,AF是高,填空:
(1)BE= =
(2)∠BAD=
(3)∠AFB= =90°
(4)S△ABC= S△ABE.

-
科目: 来源: 题型:
查看答案和解析>>【题目】有
 筐白菜,以每筐
筐白菜,以每筐 千克为标准,超过或不足的分别用正、负来表示,记录如下:
千克为标准,超过或不足的分别用正、负来表示,记录如下:与标准质量的差
 单位:千克
单位:千克






筐 数






(1)与标准质量比较,
 筐白菜总计超过或不足多少千克?
筐白菜总计超过或不足多少千克?(2)若白菜每千克售价
 元,则出售这
元,则出售这 筐白菜可卖多少元?
筐白菜可卖多少元? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,M、N、C三点的坐标分别为(
 ,1),(3,1),(3,0),点A为线段MN上的一个动点,连接AC,过点A作
,1),(3,1),(3,0),点A为线段MN上的一个动点,连接AC,过点A作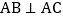 交y轴于点B,当点A从M运动到N时,点B随之运动,设点B的坐标为(0,b),则b的取值范围是( )
交y轴于点B,当点A从M运动到N时,点B随之运动,设点B的坐标为(0,b),则b的取值范围是( )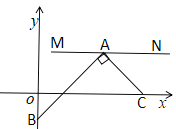
A.
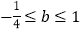 B.
B. 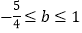 C.
C. 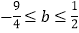 D.
D. 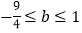
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一个长方形运动场被分隔成A,B,A,B,C共5个区,A区是边长为a m的正方形,C区是边长为c m的正方形.
(1)列式表示每个B区长方形场地的周长,并将式子化简;
(2)列式表示整个长方形运动场的周长,并将式子化简;
(3)如果a=40,c=10,求整个长方形运动场的面积.

相关试题

