【题目】如图,四边形ABCD内接于圆,对角线AC与BD相交于点E,F在AC上,AB=AD,∠BFC=∠BAD=2∠DFC.
求证:
(1)CD⊥DF;
(2)BC=2CD.

参考答案:
【答案】(1)详见解析;(2)详见解析.
【解析】
(1)利用在同圆中所对的弧相等,弦相等,所对的圆周角相等,三角形内角和可证得∠CDF=90°,则CD⊥DF;
(2)应先找到BC的一半,证明BC的一半和CD相等即可.
证明:(1)∵AB=AD,
∴弧AB=弧AD,∠ADB=∠ABD.
∵∠ACB=∠ADB,∠ACD=∠ABD,
∴∠ACB=∠ADB=∠ABD=∠ACD.
∴∠ADB=(180°﹣∠BAD)÷2=90°﹣∠DFC.
∴∠ADB+∠DFC=90°,即∠ACD+∠DFC=90°,
∴CD⊥DF.
(2)过F作FG⊥BC于点G,
∵∠ACB=∠ADB,
又∵∠BFC=∠BAD,
∴∠FBC=∠ABD=∠ADB=∠ACB.
∴FB=FC.
∴FG平分BC,G为BC中点,![]()
∵在△FGC和△DFC中,
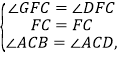
∴△FGC≌△DFC(ASA),
∴![]()
∴BC=2CD.
-
科目: 来源: 题型:
查看答案和解析>>【题目】楼房AB后有一假山,其坡度为i=1:
 ,山坡坡面上E点处有一休息亭,测得假山坡脚C与楼房水平距离BC=30米,与亭子距离CE=18米,小丽从楼房顶测得E点的俯角为45°,求楼房AB的高.(注:坡度i是指坡面的铅直高度与水平宽度的比)
,山坡坡面上E点处有一休息亭,测得假山坡脚C与楼房水平距离BC=30米,与亭子距离CE=18米,小丽从楼房顶测得E点的俯角为45°,求楼房AB的高.(注:坡度i是指坡面的铅直高度与水平宽度的比)
-
科目: 来源: 题型:
查看答案和解析>>【题目】尊老助老是中华民族的传统美德,我校的小艾同学在今年元旦节前往家附近的敬老院,为老人们表演节目送上新年的祝福,当小艾同学到达敬老院时,发现拷音乐的U盘没有带,于是边打电话给爸爸边往家走,请爸爸能帮忙送来. 3分钟后,爸爸在家找到了U盘并立即前往敬老院,相遇后爸爸将U盘交给小艾,小艾立即把速度提高到之前的1.5倍跑回敬老院,这时爸爸遇到了朋友,停下与朋友交谈了2分钟后,爸爸以原来的速度前往敬老院观看小艾的表演.爸爸与小艾的距离
 (米)与小艾从敬老院出发的时间
(米)与小艾从敬老院出发的时间 (分)之间的关系如图所示,则当小艾回到敬老院时,爸爸离敬老院还有______米.
(分)之间的关系如图所示,则当小艾回到敬老院时,爸爸离敬老院还有______米.
-
科目: 来源: 题型:
查看答案和解析>>【题目】“元旦”期间小明去永辉超市购物,恰逢永辉超市“满1400减99元”促销活动,小明准备提前购置一些年货
 和
和 ,已知
,已知 和
和 的单价总和是100到200之间的整数,小明粗略测算了一下发现自己所购年货总价为1305元,不能达到超市的促销活动金额. 于是小明又购买了
的单价总和是100到200之间的整数,小明粗略测算了一下发现自己所购年货总价为1305元,不能达到超市的促销活动金额. 于是小明又购买了 、
、 各一件,这样就能参加超市的促销活动,最后刚好付款1305元. 小明经仔细计算发现前面粗略测算时把
各一件,这样就能参加超市的促销活动,最后刚好付款1305元. 小明经仔细计算发现前面粗略测算时把 和
和 的单价看反了,那么小明实际总共买了______件年货.
的单价看反了,那么小明实际总共买了______件年货. -
科目: 来源: 题型:
查看答案和解析>>【题目】阅读材料: 小明在学习二次根式后,发现一些含根号的式子可以写成另一个式子的平方,如:
 ,善于思考的小明进行了以下探索:
,善于思考的小明进行了以下探索:设
 (其中
(其中 均为整数),则有
均为整数),则有 .
.∴
 .这样小明就找到了一种把部分
.这样小明就找到了一种把部分 的式子化为平方式的方法.
的式子化为平方式的方法.请你仿照小明的方法探索并解决下列问题:
当
 均为正整数时,若
均为正整数时,若 ,用含m、n的式子分别表示
,用含m、n的式子分别表示 ,得
,得 = ,
= , = ;
= ;(2)利用所探索的结论,找一组正整数
 ,填空: + =( +
,填空: + =( +  )2;
)2;(3)若
 ,且
,且 均为正整数,求
均为正整数,求 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】重庆一中开展了“爱生活爱运动”的活动,以鼓励学生积极参与体育锻炼.为了解学生每周体育锻炼时间,学校在活动之前对八年级同学进行了抽样调査,并根据调査结果将学生每周的体育锻炼时间分为3小时、4小时、5小时、6小时、7小时共五种情况.小明根据调查结构制作了如下两幅统计图,请你结合图中所给信息解答下列问题:
(整理数据)

“爱生活·爱运动”的活动结束之后,再次抽查这部分学生的体育锻炼时间:
一周体育锻炼时间(小时)
3
4
5
6
7
人数
3
5
15

10
(分析数据)
活动之后部分学生体育锻炼时间的统计表
平均数
中位数
众数
活动之前锻炼时间(小时)
5
5
5
活动之后锻炼时间(小时)
5.52


请根据调查信息
(1)补全条形统计图,并计算
 _____小时,
_____小时, ______小时,
______小时, _____小时;
_____小时;(2)小亮同学在活动之前与活动之后的这两次调查中,体育锻炼时间均为5小时,根据体育锻炼时间由多到少进行排名统计,请问他在被调查同学中体育锻炼时间排名靠前的是_________(填“活动之前”或“活动之后”),理由是_________________________________.
(3)已知八年级共2000名学生,请估算全年级学生在活动结束后,每周体育锻炼时间至少有6小时的学生人数有多少人?
-
科目: 来源: 题型:
查看答案和解析>>【题目】在初中阶段的函数学习中,我们经历了“确定函数的表达式——利用函数图象研究其性质——运用函数解决问题”的学习过程. 在画函数图象时,我们通过描点、平移、对称的方法画出了所学的函数图象. 同时,我们也学习了绝对值的意义
 ,结合上面经历的学习过程,现在来解决下面的问题
,结合上面经历的学习过程,现在来解决下面的问题在函数
 中,自变量
中,自变量 的取值范围是全体实数,下表是
的取值范围是全体实数,下表是 与
与 的几组对应值:
的几组对应值:

0
1
2
3
y
…
0
1
2
3
2
…
(1)根据表格填写:
 _______.
_______. (2)化简函数解析式:
当
 时,
时, _______;
_______;当
 时,
时, ______.
______.(3)在给出的平面直角坐标系中,请用你喜欢的方法画出这个函数的图象并解决以下问题;
①该函数的最大值为_______.
②若
 为该函数图象上不同的两点,则
为该函数图象上不同的两点,则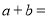 ________.
________.③根据图象可得关于
 的方程
的方程 的解为_______.
的解为_______.
相关试题

