【题目】在△ABC中,AB、BC、AC三边的长分别为![]() 、
、![]() 、
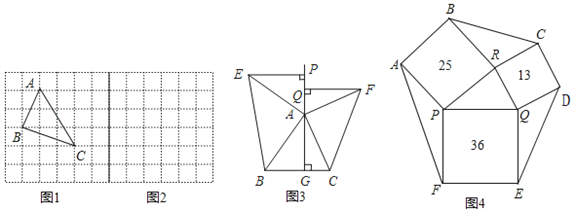
、![]() ,求这个三角形的面积.小华同学在解答这道题时,先画一个正方形网格(每个小正方形的边长为1),再在网格中画出格点△ABC(即△ABC三个顶点都在小正方形的顶点处),如图1所示.这样不需求△ABC的高,而借用网格就能计算出它的面积.这种方法叫做构图法.
,求这个三角形的面积.小华同学在解答这道题时,先画一个正方形网格(每个小正方形的边长为1),再在网格中画出格点△ABC(即△ABC三个顶点都在小正方形的顶点处),如图1所示.这样不需求△ABC的高,而借用网格就能计算出它的面积.这种方法叫做构图法.
(1)△ABC的面积为: .
(2)若△DEF三边的长分别为![]() 、
、![]() 、
、![]() ,请在图2的正方形网格中画出相应的△DEF,并利用构图法求出它的面积为 .
,请在图2的正方形网格中画出相应的△DEF,并利用构图法求出它的面积为 .
(3)如图3,△ABC中,AG⊥BC于点G,以A为直角顶点,分别以AB、AC为直角边,向△ABC外作等腰Rt△ABE和等腰Rt△ACF,过点E、F作射线GA的垂线,垂足分别为P、Q.试探究EP与FQ之间的数量关系,并证明你的结论.
(4)如图4,一个六边形的花坛被分割成7个部分,其中正方形PRBA,RQDC,QPFE的面积分别为13m2、25m2、36m2,则六边形花坛ABCDEF的面积是 m2.
参考答案:
【答案】(1)3.5;(2)3; (3)EP=FQ,证明见解析;(4)110m.
【解析】分析:(1)利用△ABC所在的正方形的面积减去四周三个小直角三角形的面积,计算即可得解;
(2)根据网格结构和勾股定理作出△DEF,再利用△DEF所在的矩形的面积减去四周三个小直角三角形的面积,计算即可得解;(3)利用同角的余角相等求出∠BAG=∠AEP,然后利用“角角边”证明△ABG和△EAP全等,同理可证△ACG和△FAQ全等,根据全等三角形对应边相等可得EP=AG=FQ;(4)过R作RH⊥PQ于H,设PH=h,在Rt△PRH和Rt△RQH中,利用勾股定理列式表示出PQ,然后解无理方程求出h,从而求出△PQR的面积,再根据六边形被分成的四个三角形的面积相等,总面积等于各部分的面积之和列式计算即可得解.
本题解析:
(1)△ABC的面积=3×3![]() ×2×1
×2×1![]() ×3×1
×3×1![]() ×2×3=911.53=95.5=3.5;
×2×3=911.53=95.5=3.5;
(2)△DEF如图2所示:

面积=2×4![]() ×1×2
×1×2![]() ×2×2
×2×2![]() ×1×4=8122=85=3;
×1×4=8122=85=3;
(3) EP=FQ,
证明:∵△ABE是等腰直角三角形,∴AB=AE,∠BAE=90,
∴∠PAE+∠BAG=180°90°=90°,又∵∠AEP+∠PAE=90°,∴∠BAG=∠AEP,
在△ABG和△EAP中,
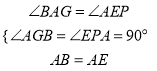 ,∴△ABG≌△EAP(AAS),同理可证,△ACG≌△FAQ,∴EP=AG=FQ;
,∴△ABG≌△EAP(AAS),同理可证,△ACG≌△FAQ,∴EP=AG=FQ;
(4)如图4,过R作RH⊥PQ于H,设RH=h,

在Rt△PRH中,PH=![]() ,
,
在Rt△RQH中,QH=![]() ,
,
∴PQ=![]() =6,
=6,
![]() ,
,
两边平方得,25h=3612![]() +13h,
+13h,
整理得, ![]() =2,
=2,
两边平方得,13h=4,
解得h=3,
∴![]() ×6×3=9,
×6×3=9,
∴六边形花坛ABCDEF的面积=25+13+36+4×9=74+36=110m.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列事件为不可能事件的是( )
A. 掷一枚质地均匀的正方体骰子,掷得的点数不是奇数就是偶数
B. 从一副扑克牌中任意抽出一张,花色是黑桃
C. 抛一枚普通的硬币,正面朝上
D. 从装满红球的袋子中摸出一个白球
-
科目: 来源: 题型:
查看答案和解析>>【题目】根据中心对称图形的性质可知,任何一对对应点的连线的就是该中心对称图形的对称中心,或两对对应点的连线的是对称中心
-
科目: 来源: 题型:
查看答案和解析>>【题目】(2016 广东省茂名市第22题)如图,一次函数y=x+b的图象与反比例函数y=
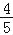 (k为常数,k≠0)的图象交于点A(﹣1,4)和点B(a,1).
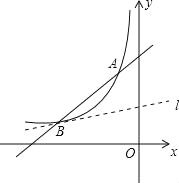
(k为常数,k≠0)的图象交于点A(﹣1,4)和点B(a,1).(1)求反比例函数的表达式和a、b的值;
(2)若A、O两点关于直线l对称,请连接AO,并求出直线l与线段AO的交点坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一个多边形,它的内角和比外角和的4倍多180°,求这个多边形的边数及内角和度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:
①
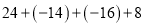 ;
; ②
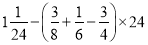 ;
;③
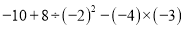 ;
; ④
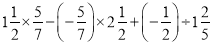 ;
;化简: ⑤
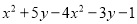 ;
; ⑥7a+3(a-3b)-2(b-3a) .
-
科目: 来源: 题型:
查看答案和解析>>【题目】(-3)×2的结果是( )
A. -5 B. 1 C. -6 D. 6
相关试题

