【题目】已知反比例函数y=![]() 的图象过点A(3,4),求反比例函数的解析式,并判断点B(6,2)是否在该反比例函数的图象上.
的图象过点A(3,4),求反比例函数的解析式,并判断点B(6,2)是否在该反比例函数的图象上.
参考答案:
【答案】反比例函数解析式为y=![]() ;B(6,2)在这个函数的图象上.
;B(6,2)在这个函数的图象上.
【解析】
试题分析:(1)首先设这个反比例函数的解析式为y=![]() (k≠0),再把点A(3,4)的坐标代入函数关系式,即可算出k的值,进而可得函数关系式;
(k≠0),再把点A(3,4)的坐标代入函数关系式,即可算出k的值,进而可得函数关系式;
(2)只要把点B(6,2)代入(1)中算求的函数关系式,满足关系式,就是函数图象上的点,反之则不在.
解:(1)设这个反比例函数的解析式为y=![]() (k≠0),依题意得:
(k≠0),依题意得:
4=![]() ,
,
所以k=12,
这个反比例函数解析式为y=![]() ;
;
(2)由(1)求得:y=![]() ,
,
当x=6时,y=2,
所以B(6,2)在这个函数的图象上.
-
科目: 来源: 题型:
查看答案和解析>>【题目】综合与探究:如图,已知抛物线y=-x2+bx+c与一直线相交于A(-1,0),C (2,3)两点,与y轴交于点N,其顶点为D 。
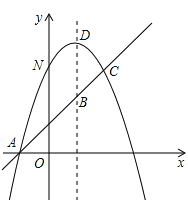
(1)确定抛物线及直线AC的函数关系式;
(2)点M在直线x =3上,求使 MN+MD 的值最小时的M点坐标;
(3)若抛物线的对称轴与直线AC 相交于点B,E 为直线AC 上的任意一点,过点E 作EF∥BD 交抛物线于点F,以B、D、E、F 为顶点的四边形能否为平行四边形?若能,求点E 的坐标;若不能,请说明理由。
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点A(a,b)是双曲线y=
 (x>0)上的一点,点P是x轴负半轴上的一动点,AC⊥y轴于点C,过点A作AD⊥x轴于点D,连接AP交y轴于点B.
(x>0)上的一点,点P是x轴负半轴上的一动点,AC⊥y轴于点C,过点A作AD⊥x轴于点D,连接AP交y轴于点B.
(1)△PAC的面积是 ;
(2)当a=2,点P的坐标为(﹣2,0)时,求△ACB的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图AB∥CD.∠1=∠2,∠3=∠4,试说明AD∥BE.

解:∵AB∥CD(已知)
∴∠4=∠ ( )
∵∠3=∠4(已知)
∴∠3=∠ ( )
∵∠1=∠2(已知)
∴∠1+∠CAF=∠2+∠CAF(
即∠ =∠ ( )
∴∠3=∠
∴AD∥BE( )
-
科目: 来源: 题型:
查看答案和解析>>【题目】一个正多边形的每个外角都等于36°,那么它是( )
A.正六边形 B.正八边形 C.正十边形 D.正十二边形
-
科目: 来源: 题型:
查看答案和解析>>【题目】在2,﹣2,3,﹣3这四个数中,最小的数是( )
A. 2 B. -2 C. 3 D. ﹣3
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在直角坐标系中,点A、B的坐标分别为(1,4)和(3,0),点C是y轴上的一个动点,且A、B、C三点不在同一条直线上,当△ABC的周长最小时,点C的坐标是( )
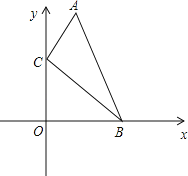
A.(0,0) B.(0,1) C.(0,2) D.(0,3)
相关试题

