【题目】如图,点A(a,b)是双曲线y=![]() (x>0)上的一点,点P是x轴负半轴上的一动点,AC⊥y轴于点C,过点A作AD⊥x轴于点D,连接AP交y轴于点B.
(x>0)上的一点,点P是x轴负半轴上的一动点,AC⊥y轴于点C,过点A作AD⊥x轴于点D,连接AP交y轴于点B.

(1)△PAC的面积是 ;
(2)当a=2,点P的坐标为(﹣2,0)时,求△ACB的面积.
参考答案:
【答案】(1)4;(2)2.
【解析】
试题分析:(1)由点A(a,b)是双曲线y=![]() (x>0)上,得到ab=8,根据反比例函数系数k的几何意义,就看得到△PAC的面积=
(x>0)上,得到ab=8,根据反比例函数系数k的几何意义,就看得到△PAC的面积=![]() ADAC=
ADAC=![]() ab=4;
ab=4;
(2)先求出直线AP的解析式为y=x+2,得到B(0,2),即可求出S△ABC=![]() ACBC=
ACBC=![]() ×2×2=2.
×2×2=2.
解:(1)∵点A(a,b)是双曲线y=![]() (x>0)上,
(x>0)上,
∴ab=8,
∵AC⊥y轴于C点,AD⊥x轴于D点,
∴AC=a,AD=b,
∴△PAC的面积=![]() ADAC=
ADAC=![]() ab=4;
ab=4;
故答案为:4;
(2)∵a=2,
∴b=4,
∴AC=2,AD=4,A(2,4),
设直线AP的解析式为y=kx+b,
∴![]() ,
,
∴![]() ,
,
∴直线AP的解析式为y=x+2,
∴B(0,2),
∴S△ABC=![]() ACBC=
ACBC=![]() ×2×2=2.
×2×2=2.
-
科目: 来源: 题型:
查看答案和解析>>【题目】服装店销售某款服装,一件服装的标价为300元,若按标价的八折销售,仍可获利60元,则这款服装每件的进价为__________元.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知等腰三角形的两边长分别为5和6,则这个等腰三角形的周长为( )
A.11
B.16
C.17
D.16或17 -
科目: 来源: 题型:
查看答案和解析>>【题目】综合与探究:如图,已知抛物线y=-x2+bx+c与一直线相交于A(-1,0),C (2,3)两点,与y轴交于点N,其顶点为D 。
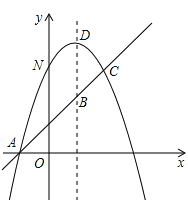
(1)确定抛物线及直线AC的函数关系式;
(2)点M在直线x =3上,求使 MN+MD 的值最小时的M点坐标;
(3)若抛物线的对称轴与直线AC 相交于点B,E 为直线AC 上的任意一点,过点E 作EF∥BD 交抛物线于点F,以B、D、E、F 为顶点的四边形能否为平行四边形?若能,求点E 的坐标;若不能,请说明理由。
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图AB∥CD.∠1=∠2,∠3=∠4,试说明AD∥BE.

解:∵AB∥CD(已知)
∴∠4=∠ ( )
∵∠3=∠4(已知)
∴∠3=∠ ( )
∵∠1=∠2(已知)
∴∠1+∠CAF=∠2+∠CAF(
即∠ =∠ ( )
∴∠3=∠
∴AD∥BE( )
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知反比例函数y=
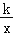 的图象过点A(3,4),求反比例函数的解析式,并判断点B(6,2)是否在该反比例函数的图象上.
的图象过点A(3,4),求反比例函数的解析式,并判断点B(6,2)是否在该反比例函数的图象上. -
科目: 来源: 题型:
查看答案和解析>>【题目】一个正多边形的每个外角都等于36°,那么它是( )
A.正六边形 B.正八边形 C.正十边形 D.正十二边形
相关试题

