【题目】如图，已知等腰三角形ABC中，AB=AC，点D,E分别在边AB、AC上，且AD=AE，连接BE、CD，交于点F.

(1)求证：∠ABE＝∠ACD；

(2)求证：过点A、F的直线垂直平分线段BC.

参考答案：

【答案】(1)证明详见解析(2) 证明详见解析

【解析】

（1）证得△ABE≌△ACD后利用全等三角形的对应角相等即可证得结论；

（2）利用垂直平分线段的性质即可证得结论．

（1）在△ABE和△ACD中，

，

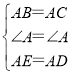∴△ABE≌△ACD，

∴∠ABE=∠ACD；

（2）连接AF．

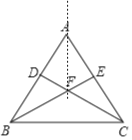
∵AB=AC，

∴∠ABC=∠ACB，

由（1）可知∠ABE=∠ACD，

∴∠FBC=∠FCB，

∴FB=FC，

∵AB=AC，

∴点A、F均在线段BC的垂直平分线上，

即直线AF垂直平分线段BC．

关闭