搜索
【题目】如图，∠BAP＋∠APD＝180°，∠AOE＝∠1，∠FOP＝∠2.
(1)若∠1＝55°，求∠2的度数；
(2)求证：AE∥FP.
参考答案：
【答案】(1)∠2＝55°；(2)证明见解析.
【解析】
（1）利用∠AOE＝∠FOP来等量替换，再求出∠2的度数；（2）证出∠EAO＝∠FPO即可说明AE∥FP.
(1)∵∠AOE＝∠1，∠FOP＝∠2，
又∵∠AOE＝∠FOP(对顶角相等)，
∴∠1＝∠2.
∵∠1＝55°，
∴∠2＝55°.
(2)证明：∵∠BAP＋∠APD＝180°，
∴AB∥CD(同旁内角互补，两直线平行)．
∴∠BAP＝∠APC(两直线平行，内错角相等)．
∵∠1＝∠2，
∴∠EAO＝∠FPO.
∴AE∥PF(内错角相等，两直线平行)．
-
科目： 来源： 题型：
查看答案和解析>>【题目】阅读下面材料：
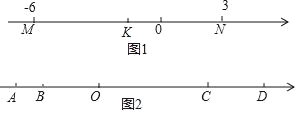
如图1，在数轴上点M表示的数是﹣6，点N表示的数是3，求线段MN的中点K所示的数．
对于求中点表示数的问题，只要用点N所表示的数3，加上点M所表示的数﹣6，得到的结果再除以2，就可以得到中点K所表示的数；即K点表示的数为
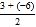=﹣1.5利用材料中知识解决下面问题：
如图2，已知数轴上有A、B、C、D四点，A点表示数为﹣6，B点表示的数是﹣4，线段AD=18，BC=3CD．
(1)点D所表示的数是 ；
(2)若点B以每秒4个单位的速度向右运动，点D以每秒1个单位的速度向左运动，同时运动t秒后，当点C为线段BD的中点时，求t的值；
(3)若(2)中点B、点D的运动速度运动方向不变，点A以每秒10个单位的速度向右运动，点C以每秒3个单位的速度向左运动，点P是线段AC的中点，点Q是线段BD的中点，A、B、C、D四点同时运动，运动时间为t，求线段PQ的长（用含t的式子表示）．
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知AB∥CD，点E为AB，CD之外任意一点．
(1)如图1，探究∠BED与∠B，∠D的数量关系，并说明理由；
(2)如图2，探究∠CDE与∠B，∠E的数量关系，并说明理由．
-
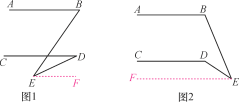
科目： 来源： 题型：
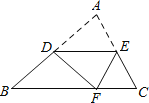
查看答案和解析>>【题目】如图，在△ABC中，∠A=70°∠B=50°，点D，E分别为AB，AC上的点，沿DE折叠，使点A落在BC边上点F处，若△EFC为直角三角形，则∠BDF的度数为______．
-
科目： 来源： 题型：
查看答案和解析>>【题目】命题“两直线平行，内错角的平分线互相平行”是真命题吗？如果是，请给出证明；如果不是，请举出反例．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在平面直角坐标系中有Rt△ABC，已知∠CAB=90°，AB=AC，A（﹣2，0），B（0，1）．
（1）点C的坐标是；
（2）将△ABC沿x轴正方向平移得到△A′B′C′，且B，C两点的对应点B′，C′恰好落在反比例函数y=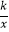
的图象上，求该反比例函数的解析式． -
科目： 来源： 题型：
查看答案和解析>>【题目】学生骑电动车上学给交通安全带来隐患，为了解某中学2 500个学生家长对“中学生骑电动车上学”的态度，中随机调查400个家长，结果有360个家长持反对态度，则下列说法正确的是( )
A. 调查方式是全面调查 B. 样本容量是360
C. 该校只有360个家长持反对态度 D. 该校约有90%的家长持反对态度
相关试题
