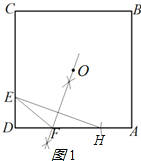
【题目】(1)如图1,△ABC中,∠C=90°,AB的垂直平分线交AC于点D,连接BD. 若AC=2,BC=1,则△BCD的周长为___________________.
(2)O为正方形ABCD的中心,E为CD边上一点,F为AD边上一点,且△EDF的周长等于AD的长.
①在图2中求作△EDF.(要求:尺规作图,不写作法,保留作图痕迹)
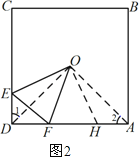
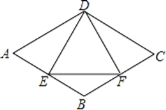
②在图3中补全图形,求∠EOF的度数.
③若![]() ,则
,则![]() =_______________.
=_______________.

图1 图2 图3
参考答案:
【答案】(1)3;(2)①作图见解析;②45°;③![]() .
.
【解析】试题分析:(1)由线段垂直平分线的性质得出BD=AD,得出△BCD的周长=BC+CD+BD=BC+AC,即可得出结果;
(2)①在AD上截取AH=DE,再作EG的垂直平分线,交AD于F,△EDF即为所求;
②连接OA、OD、OH,由正方形的性质得出∠1=∠2=45°,由SAS证明△ODE≌△OAH,得出∠DOE=∠AOH,OE=OH,得出∠EOH=90°,证出EF=HF,由SSS证明△EOF≌△HOF,得出∠EOF=∠HOF=45°即可;
③作OG⊥CD于G,OK⊥AD于K,设AF=8t,则CE=9t,设OG=m,由正方形的性质得出GE=CE-CG=9t-m,DE=2CG-CE=2m-9t,FK=AF-KA=8t-m,DF=2DK-AF=2m-8t,由HL证明Rt△EOG≌Rt△HOK,得出GE=KH,因此EF=GE+FK=17t-2m,由勾股定理得出方程,解方程求出m=6t,得出OG=OK=6t,GE=9t-m=9t-6t=3t,FK=8t-m=2t,由勾股定理即可得出结果.
试题解析:(1)∵AB的垂直平分线交AC于点D,
∴BD=AD,
∴△BCD的周长=BC+CD+BD=BC+AC=1+2=3,
故答案为:3;
(2)①如图1所示:△EDF即为所求;
②如图2所示:
AH=DE,连接OA、OD、OH,
∵点O为正方形ABCD的中心,
∴OA=OD,∠AOD=90°,∠1=∠2=45°,
在△ODE和△OAH中,
 ,
,
∴△ODE≌△OAH(SAS),
∴∠DOE=∠AOH,OE=OH,
∴∠EOH=90°,
∵△EDF的周长等于AD的长,
∴EF=HF,
在△EOF和△HOF中,
 ,
,
∴△EOF≌△HOF(SSS),
∴∠EOF=∠HOF=45°;
③作OG⊥CD于G,OK⊥AD于K,如图3所示:

设AF=8t,则CE=9t,设OG=m,
∵O为正方形ABCD的中心,
∴四边形OGDK为正方形,CG=DG=DK=KA=![]() AB=OG,
AB=OG,
∴GE=CE﹣CG=9t﹣m,DE=2CG﹣CE=2m﹣9t,FK=AF﹣KA=8t﹣m,DF=2DK﹣AF=2m﹣8t,
由(2)②知△EOF≌△HOF,
∴OE=OH,EF=FH,
在Rt△EOG和Rt△HOK中,
![]() ,
,
∴Rt△EOG≌Rt△HOK(HL),
∴GE=KH,
∴EF=GE+FK=9t﹣m+8t﹣m=17t﹣2m,
由勾股定理得:DE2+DF2=EF2,
∴(2m﹣9t)2+(2m﹣8t)2=(17t﹣2m)2,
整理得:(m+6t)(m﹣6t)=0,
∴m=6t,
∴OG=OK=6t,GE=9t﹣m=9t﹣6t=3t,FK=8t﹣m=2t,
∴ =
=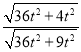 =
=![]() =
=![]() .
.
故答案为![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】列方程式应用题.
天河食品公司收购了200吨新鲜柿子,保质期15天,该公司有两种加工技术,一种是加工为普通柿饼,另一种是加工为特级霜降柿饼,也可以不需加工直接销售.相关信息见表:
品种
每天可加工数量(吨)
每吨获利(元)
新鲜柿子
不需加工
1000元
普通柿饼
16吨
5000元
特级霜降柿饼
8吨
8000元
由于生产条件的限制,两种加工方式不能同时进行,为此公司研制了两种可行方案:
方案1:尽可能多地生产为特级霜降柿饼,没来得及加工的新鲜柿子,在市场上直接销售;
方案2:先将部分新鲜柿子加工为特级霜降柿饼,再将剩余的新鲜柿子加工为普通柿饼,恰好15天完成.
请问:哪种方案获利更多?获利多少元?
-
科目: 来源: 题型:
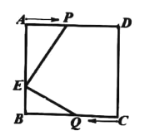
查看答案和解析>>【题目】如图,欢欢和乐乐分别站在正方形
 的顶点
的顶点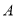 和顶点
和顶点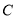 处,欢欢以
处,欢欢以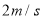 的速度走向终点
的速度走向终点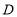 ,途中位置记为点
,途中位置记为点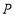 ;乐乐以
;乐乐以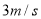 的速度走向终点
的速度走向终点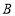 ,途中位置记为
,途中位置记为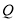 .假设两人同时出发,两人都到达终点时结束运动.已知正方形边长为
.假设两人同时出发,两人都到达终点时结束运动.已知正方形边长为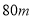 ,点
,点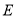 在
在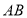 上,
上,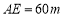 .记三角形
.记三角形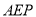 的面积为
的面积为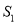 ,三角形
,三角形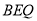 的面积为
的面积为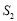 .设出发时间为
.设出发时间为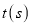 :
:
(1)如图情况,用含
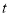 的代数式表示下列线段的长度:
的代数式表示下列线段的长度: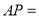 ______;
______;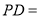 ______;
______; 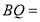 ______;
______;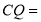 ______;
______;(2)如图情况,他们出发多少秒后
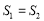 ?
?(3)是否存在这样的时刻
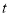 ,使得
,使得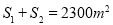 ?若存在,请求出
?若存在,请求出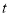 的最小值,若不存在,请说明理由.
的最小值,若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】在星期一的第八节课,我校体育老师随机抽取了九年级的总分学生进行体育中考的模拟测试,并对成绩进行统计分析,绘制了频数分布表和统计图,按得分划分成A、B、C、D、E、F六个等级,并绘制成如下两幅不完整的统计图表.
等级
得分x(分)
频数(人)
A
95<x≤100
4
B
90<x≤95
m
C
85<x≤90
n
D
80<x≤85
24
E
75<x≤80
8
F
70<x≤75
4
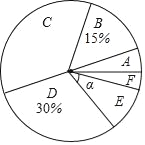
请你根据图表中的信息完成下列问题:
1)本次抽样调查的样本容量是 .其中m= ,n= .
2)扇形统计图中,求E等级对应扇形的圆心角α的度数;
3)我校九年级共有700名学生,估计体育测试成绩在A、B两个等级的人数共有多少人?
4)我校决定从本次抽取的A等级学生(记为甲、乙、丙、丁)中,随机选择2名成为学校代表参加全市体能竞赛,请你用列表法或画树状图的方法,求恰好抽到甲和乙的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某小组做“用频率估计概率”的试验时,统计了某一结果出现的频率,绘制了如图所示的折线统计图,则符合这一结果的试验最有可能的是( )

A. 在“石头、剪刀、布”的游戏中,小明随机出的是“剪刀”
B. 一副去掉大小王的普通扑克牌洗匀后,从中任抽一张牌的花色是红桃
C. 暗箱中有1个红球和2个黄球,它们只有颜色上的区别,从中任取一球是黄球
D. 掷一个质地均匀的正六面体骰子,向上的面点数是4
-
科目: 来源: 题型:
查看答案和解析>>【题目】某自行车厂计划平均每天生产200辆,但是由于种种原因,实际每天生产量与计划量相比有出入。表是某周的生产情况(超产记为正,减产记为负):

(1)根据记录的数据可知该厂星期三生产自行车多少辆?
(2)产量最多的一天比产量最少的一天多生产自行车多少辆?
(3)根据记录的数据可知该厂本周实际共生产自行车多少辆?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在菱形ABCD中,E是AB边上一点,且∠A=∠EDF=60°,有下列结论:①AE=BF;②△DEF是等边三角形;③△BEF是等腰三角形;④∠ADE=∠BEF,其中结论正确的个数是( )
A.3
B.4
C.1
D.2
相关试题

