【题目】矩形的两条对角线的夹角为60度,对角线长为15,则矩形的较短边长为( )
A. 12B. 10C. 7.5D. 5
参考答案:
【答案】C
【解析】
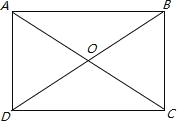
如图所示:∠AOD=∠BOC=60°,即:∠COD=120°>∠AOD=60°,AD是该矩形较短的一边,根据矩形的性质:矩形的对角线相等且互相平分,所以有OA=OD=OC=OB=7.5,又因为∠AOD=∠BOC=60°,所以AD的长即可求出.
如图所示:矩形ABCD,对角线AC=BD=15,∠AOD=∠BOC=60°,
∵四边形ABCD是矩形,
∴OA=OD=OC=OB=![]() ×15=7.5(矩形的对角线互相平分且相等),
×15=7.5(矩形的对角线互相平分且相等),
又∵∠AOD=∠BOC=60°,
∴OA=OD=AD=7.5,
∵∠COD=120°>∠AOD=60°,
∴AD<DC,
所以该矩形较短的一边长为7.5,
故选C.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知BC是⊙O的直径,点D为BC延长线上的一点,点A为圆上一点,且AB=AD,AC=CD.

(1)求证:△ACD∽△BAD;
(2)求证:AD是⊙O的切线. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,Rt△ABC的斜边AB在y轴上,边AC与x轴交于点D,AE平分∠BAC交边BC于点E,经过点A、D、E的圆的圆心F恰好在y轴上,⊙F与y轴相交于另一点G.

(1)求证:BC是⊙F的切线;
(2)若点A、D的坐标分别为A(0,﹣1),D(2,0),求⊙F的半径;
(3)试探究线段AG、AD、CD三者之间满足的等量关系,并证明你的结论. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,在矩形ABCD中,E是CB延长线上一个动点,F、G分别为AE、BC的中点,FG与ED相交于点H
(1) 求证:HE=HG
(2) 如图2,当BE=AB时,过点A作AP⊥DE于点P连接BP,求
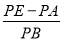 的值
的值(3) 在(2)的条件下,若AD=2,∠ADE=30°,则BP的长为______________


-
科目: 来源: 题型:
查看答案和解析>>【题目】下列命题中,正确的个数是 ( )
①若三条线段的比为1:1:
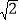 ,则它们组成一个等腰直角三角形;②两条对角线相等的平行四边形是矩形;③对角线互相垂直的四边形是菱形;④有两个角相等的梯形是等腰梯形;⑤一条直线与矩形的一组对边相交,必分矩形为两个直角梯形。
,则它们组成一个等腰直角三角形;②两条对角线相等的平行四边形是矩形;③对角线互相垂直的四边形是菱形;④有两个角相等的梯形是等腰梯形;⑤一条直线与矩形的一组对边相交,必分矩形为两个直角梯形。A. 2个 B. 3个 C. 4个 D. 5个
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在矩形ABCD中,AB=8,BC=4,将矩形沿AC折叠,点D落在点D′处,则重叠部分△AFC的面积为( )

A.6B.8C.10D.12
-
科目: 来源: 题型:
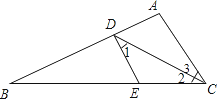
查看答案和解析>>【题目】如图,已知CD平分∠ACB,∠1=∠2.
(1)求证:DE∥AC;
(2)若∠3=30°,∠B=25°,求∠BDE的度数.
相关试题

