【题目】先化简,后求值:a(a+1)﹣(a+1)(a﹣1),其中a=3.
参考答案:
【答案】解:原式=a2+a﹣(a2﹣1) =a2+a﹣a2+1
=a+1
当a=3时,原式=3+1=4
【解析】先根据单项式乘以多项式的法则和运用平方差公式去掉括号,再合并同类项,最后将a的值代入化简后的式子就可以求出原式的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】小丽在计算一个二项式的平方时,得到正确结果m2﹣10mn+■,但最后一项不慎被墨水污染,这一项应是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】一个寻宝游戏的寻宝通道由正方形ABCD的边组成,如图1所示.为记录寻宝者的行进路线,在AB的中点M处放置了一台定位仪器,设寻宝者行进的时间为x,寻宝者与定位仪器之间的距离为y,若寻宝者匀速行进,且表示y与x的函数关系的图象大致如图2所示,则寻宝者的行进路线可能为( )

A.A→B
B.B→C
C.C→D
D.D→A -
科目: 来源: 题型:
查看答案和解析>>【题目】如图Rt△ABC中,∠ACB=90°,D为AB的中点,E在边AB上,AB=12,BC=6,当ED=
 CD,则CE= .
CD,则CE= . 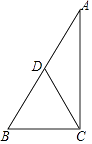
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD是正方形,边长为4,点G在边BC上运动,DE⊥AG于E,BF∥DE交AG于点F,在运动过程中存在BF+EF的最小值,则这个最小值是 .
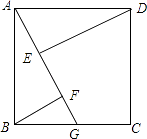
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,某日的钱塘江观测信息如下:

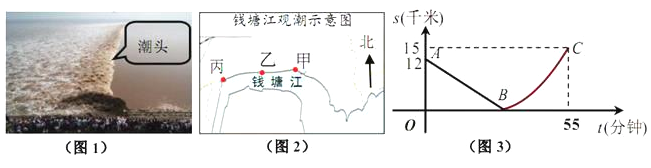
按上述信息,小红将“交叉潮”形成后潮头与乙地质检的距离
 (千米)与时间
(千米)与时间 (分钟)的函数关系用图3表示.其中:“11:40时甲地‘交叉潮’的潮头离乙地12千米”记为点
(分钟)的函数关系用图3表示.其中:“11:40时甲地‘交叉潮’的潮头离乙地12千米”记为点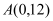 ,点
,点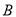 坐标为
坐标为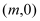 ,曲线
,曲线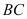 可用二次函数:s=
可用二次函数:s=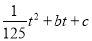 ,(
,(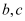 是常数)刻画.
是常数)刻画.(1)求
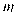 值,并求出潮头从甲地到乙地的速度;
值,并求出潮头从甲地到乙地的速度;(2)11:59时,小红骑单车从乙地出发,沿江边公路以
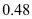 千米/分的速度往甲地方向去看潮,问她几分钟与潮头相遇?
千米/分的速度往甲地方向去看潮,问她几分钟与潮头相遇?(3)相遇后,小红立即调转车头,沿江边公路按潮头速度与潮头并行,但潮头过乙地后均匀加速,而单车最高速度为
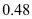 千米/分,小红逐渐落后.问小红与潮头相遇到落后潮头1.8千米共需多长时间?(潮水加速阶段速度
千米/分,小红逐渐落后.问小红与潮头相遇到落后潮头1.8千米共需多长时间?(潮水加速阶段速度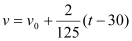 ,
, 是加速前的速度).
是加速前的速度). -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一次函数
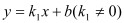 与反比例函数
与反比例函数 的图象交于点
的图象交于点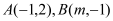 .
.(1)求这两个函数的表达式;
(2)在
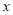 轴上是否存在点
轴上是否存在点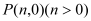 ,使
,使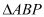 为等腰三角形?若存在,求
为等腰三角形?若存在,求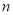 的值,若不存在,说明理由.
的值,若不存在,说明理由.
相关试题

