【题目】如图,四边形ABCD是正方形,边长为4,点G在边BC上运动,DE⊥AG于E,BF∥DE交AG于点F,在运动过程中存在BF+EF的最小值,则这个最小值是 . 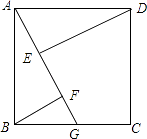
参考答案:
【答案】2 ![]()
【解析】解:∵四边形ABCD是正方形,
∴AB=AD,∠BAD=90°,
∵DE⊥AG,
∴∠AED=90°,
∴∠ADE+∠DAE=90°,
又∵∠BAF+∠DAE=∠BAD=90°,
∴∠BAF=∠ADE,
∵BF∥DE,
∴∠AED=∠BFA=90°,
在△ABF和△DAE中,
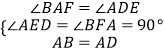 ,
,
∴△ABF≌△DAE(AAS),
∴BF=AE,AF=DE,
∴BF+EF=AE+EF=AF=DE,
∴只要求出DE的最小值即可,当G与C重合时,DE的值最小,此时DE=2 ![]() ,
,
∴BF+EF的最小值为2 ![]() .
.
所以答案是:2 ![]() .
.
【考点精析】通过灵活运用正方形的性质,掌握正方形四个角都是直角,四条边都相等;正方形的两条对角线相等,并且互相垂直平分,每条对角线平分一组对角;正方形的一条对角线把正方形分成两个全等的等腰直角三角形;正方形的对角线与边的夹角是45o;正方形的两条对角线把这个正方形分成四个全等的等腰直角三角形即可以解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一个寻宝游戏的寻宝通道由正方形ABCD的边组成,如图1所示.为记录寻宝者的行进路线,在AB的中点M处放置了一台定位仪器,设寻宝者行进的时间为x,寻宝者与定位仪器之间的距离为y,若寻宝者匀速行进,且表示y与x的函数关系的图象大致如图2所示,则寻宝者的行进路线可能为( )

A.A→B
B.B→C
C.C→D
D.D→A -
科目: 来源: 题型:
查看答案和解析>>【题目】如图Rt△ABC中,∠ACB=90°,D为AB的中点,E在边AB上,AB=12,BC=6,当ED=
 CD,则CE= .
CD,则CE= . 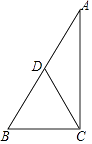
-
科目: 来源: 题型:
查看答案和解析>>【题目】先化简,后求值:a(a+1)﹣(a+1)(a﹣1),其中a=3.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,某日的钱塘江观测信息如下:

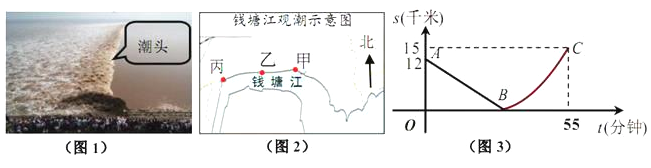
按上述信息,小红将“交叉潮”形成后潮头与乙地质检的距离
 (千米)与时间
(千米)与时间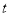 (分钟)的函数关系用图3表示.其中:“11:40时甲地‘交叉潮’的潮头离乙地12千米”记为点
(分钟)的函数关系用图3表示.其中:“11:40时甲地‘交叉潮’的潮头离乙地12千米”记为点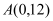 ,点
,点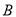 坐标为
坐标为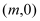 ,曲线
,曲线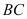 可用二次函数:s=
可用二次函数:s=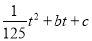 ,(
,(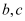 是常数)刻画.
是常数)刻画.(1)求
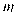 值,并求出潮头从甲地到乙地的速度;
值,并求出潮头从甲地到乙地的速度;(2)11:59时,小红骑单车从乙地出发,沿江边公路以
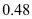 千米/分的速度往甲地方向去看潮,问她几分钟与潮头相遇?
千米/分的速度往甲地方向去看潮,问她几分钟与潮头相遇?(3)相遇后,小红立即调转车头,沿江边公路按潮头速度与潮头并行,但潮头过乙地后均匀加速,而单车最高速度为
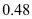 千米/分,小红逐渐落后.问小红与潮头相遇到落后潮头1.8千米共需多长时间?(潮水加速阶段速度
千米/分,小红逐渐落后.问小红与潮头相遇到落后潮头1.8千米共需多长时间?(潮水加速阶段速度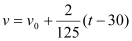 ,
, 是加速前的速度).
是加速前的速度). -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一次函数
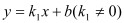 与反比例函数
与反比例函数 的图象交于点
的图象交于点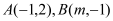 .
.(1)求这两个函数的表达式;
(2)在
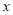 轴上是否存在点
轴上是否存在点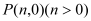 ,使
,使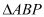 为等腰三角形?若存在,求
为等腰三角形?若存在,求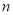 的值,若不存在,说明理由.
的值,若不存在,说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】平面直角坐标系中点(-2,1)关于x轴的对称点的坐标为()
A. (-2,-1 ) B. (2,1) C. (-1,2) D. (1,-2)
相关试题

