【题目】如图Rt△ABC中,∠ACB=90°,D为AB的中点,E在边AB上,AB=12,BC=6,当ED= ![]() CD,则CE= .
CD,则CE= . 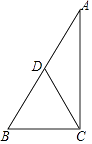
参考答案:
【答案】3 ![]() 或3
或3 ![]()
【解析】解:∵在Rt△ABC中,∠ACB=90°,D为AB的中点,AB=12,BC=6,
∴AD=BD=CD= ![]() AB=6,①如图1,E在AD上,
AB=6,①如图1,E在AD上,
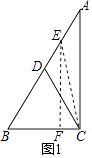
连结CE,过E点作EF⊥BC于F,
∵ED= ![]() CD,
CD,
∴DE=3,
∴BE=9,
∴BF= ![]() BE=4.5,
BE=4.5,
∴在Rt△BFE中,EF= ![]() =
= ![]() ,
,
∵CF=BC﹣BF=6﹣4.5=1.5,
∴在Rt△CFE中,CE= ![]() =3
=3 ![]() ;②如图2,E在BD上,
;②如图2,E在BD上,
连结CE,过E点作EF⊥BC于F,
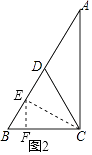
∵ED= ![]() CD,
CD,
∴DE=3,
∴BE=3,
∴BF= ![]() BE=1.5,
BE=1.5,
∴在Rt△BFE中,EF= ![]() =
= ![]() ,
,
∵CF=BC﹣BF=6﹣1.5=4.5,
∴在Rt△CFE中,CE= ![]() =3
=3 ![]() .
.
故CE=3 ![]() 或3
或3 ![]() .
.
所以答案是:3 ![]() 或3
或3 ![]() .
.
【考点精析】本题主要考查了直角三角形斜边上的中线和勾股定理的概念的相关知识点,需要掌握直角三角形斜边上的中线等于斜边的一半;直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图是小强洗漱时的侧面示意图,洗漱台(矩形
 )靠墙摆放,高
)靠墙摆放,高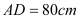 ,宽
,宽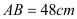 .小强身高
.小强身高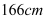 ,下半身
,下半身 ,洗漱时下半身与地面成
,洗漱时下半身与地面成 (
(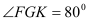 ),身体前倾成
),身体前倾成 (
(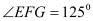 ),脚与洗漱台距离
),脚与洗漱台距离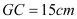 (点
(点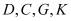 在同一直线上).
在同一直线上).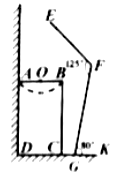
(1)此时小强头部
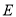 点与地面
点与地面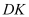 相距多少?
相距多少?(2)小强希望他的头部
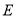 恰好在洗漱盆
恰好在洗漱盆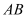 中点
中点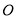 的正上方,他应向前或后退多少?
的正上方,他应向前或后退多少?(
 ,结果精确到
,结果精确到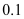 )
) -
科目: 来源: 题型:
查看答案和解析>>【题目】小丽在计算一个二项式的平方时,得到正确结果m2﹣10mn+■,但最后一项不慎被墨水污染,这一项应是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】一个寻宝游戏的寻宝通道由正方形ABCD的边组成,如图1所示.为记录寻宝者的行进路线,在AB的中点M处放置了一台定位仪器,设寻宝者行进的时间为x,寻宝者与定位仪器之间的距离为y,若寻宝者匀速行进,且表示y与x的函数关系的图象大致如图2所示,则寻宝者的行进路线可能为( )

A.A→B
B.B→C
C.C→D
D.D→A -
科目: 来源: 题型:
查看答案和解析>>【题目】先化简,后求值:a(a+1)﹣(a+1)(a﹣1),其中a=3.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD是正方形,边长为4,点G在边BC上运动,DE⊥AG于E,BF∥DE交AG于点F,在运动过程中存在BF+EF的最小值,则这个最小值是 .
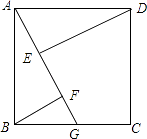
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,某日的钱塘江观测信息如下:

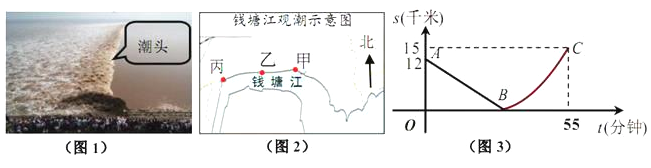
按上述信息,小红将“交叉潮”形成后潮头与乙地质检的距离
 (千米)与时间
(千米)与时间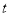 (分钟)的函数关系用图3表示.其中:“11:40时甲地‘交叉潮’的潮头离乙地12千米”记为点
(分钟)的函数关系用图3表示.其中:“11:40时甲地‘交叉潮’的潮头离乙地12千米”记为点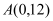 ,点
,点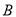 坐标为
坐标为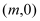 ,曲线
,曲线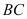 可用二次函数:s=
可用二次函数:s=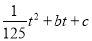 ,(
,(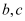 是常数)刻画.
是常数)刻画.(1)求
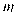 值,并求出潮头从甲地到乙地的速度;
值,并求出潮头从甲地到乙地的速度;(2)11:59时,小红骑单车从乙地出发,沿江边公路以
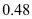 千米/分的速度往甲地方向去看潮,问她几分钟与潮头相遇?
千米/分的速度往甲地方向去看潮,问她几分钟与潮头相遇?(3)相遇后,小红立即调转车头,沿江边公路按潮头速度与潮头并行,但潮头过乙地后均匀加速,而单车最高速度为
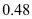 千米/分,小红逐渐落后.问小红与潮头相遇到落后潮头1.8千米共需多长时间?(潮水加速阶段速度
千米/分,小红逐渐落后.问小红与潮头相遇到落后潮头1.8千米共需多长时间?(潮水加速阶段速度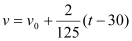 ,
, 是加速前的速度).
是加速前的速度).
相关试题

