【题目】如图,△ABC中,D为AC上一点,CD=2DA,∠BAC=45°,∠BDC=60°,CE⊥BD,E为垂足,连接AE.
求证:(1)DE=DA;(2)CE2=ADAC.
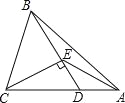
参考答案:
【答案】(1)证明见解析;(2)证明见解析.
【解析】
试题分析:(1)根据直角三角形30度角性质得到DE=![]() CD,根据已知条件AD=
CD,根据已知条件AD=![]() DC,由此不难证明.
DC,由此不难证明.
(2)先证明∠ECA=∠EAC=∠AED=30°,再证明△DEA∽△ECA即可.
试题解析:(1)∵CE⊥BD,∠BDC=60°
∴∠ECD=30°,
∴DE=![]() CD,又∵CD=2DA,即DA=
CD,又∵CD=2DA,即DA=![]() CD,
CD,
∴ED=DA.
(2)∵∠EDC=60°=∠DEA+∠DAE,
∵DE=DA,
∴∠DEA=∠DAE=30°,
∵∠ECD=30°,
∴∠ECA=∠EAC=∠AED=30°,
∴EC=EA,
∵∠EAD=∠CAE,∠AED=∠ACE
∴△DEA∽△ECA,
∴![]() ,
,
∴AE2=ADAC,∴EA=EC,
∴EC2=ADAC.
-
科目: 来源: 题型:
查看答案和解析>>【题目】用配方法解一元二次方程x2+2x﹣3=0 时,方程变形正确的是_____(填序号)
①(x﹣1)2=2 ②(x+1)2=4 ③(x﹣1)2=1④(x+1)2=7.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某红外线遥控器发出的红外线波长为0.00 000 094米,用科学记数法表示这个数是()
A. 9.4×10-10B. 9.4×10-9C. 9.4×10-8D. 9.4×10-7
-
科目: 来源: 题型:
查看答案和解析>>【题目】若等腰三角形的两边的边长分别为10cm和5cm,则第三边的长是cm.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知二次函数y=ax2+bx+c(a≠0)的图象经过点A(1,0),B(2,0),C(0,-2),直线x=m(m>2)与x轴交于点D.
(1)求二次函数的解析式;
(2)在直线x=m(m>2)上有一点E(点E在第四象限),使得E、D、B为顶点的三角形与以A、O、C为顶点的三角形相似,求E点坐标(用含m的代数式表示).
-
科目: 来源: 题型:
查看答案和解析>>【题目】一鱼池里有鲤鱼,鲫鱼,鲢鱼共1000尾,一渔民通过多次捕捞试验后发现,鲤鱼,鲫鱼出现的概率约为31%和42%,则这个鱼池里大概有鲤鱼______尾,鲫鱼______尾,鲢鱼______尾.
-
科目: 来源: 题型:
查看答案和解析>>【题目】抛物线y=﹣2(x+1)2+3的顶点坐标是( )
A.(1,3) B.(﹣1,﹣3) C.(﹣2,3) D.(﹣1,3)
相关试题

