【题目】如图,AB是⊙O的直径,C是⊙O上一点,D在AB的延长线上,且∠BCD=∠A.
(1)求证:CD是⊙O的切线;
(2)若⊙O的半径为3,CD=4,求BD的长.

参考答案:
【答案】(1)证明见解析(2)2
【解析】
试题分析:(1)连接OC,由AB是⊙O的直径可得出∠ACB=90°,即∠ACO+∠OCB=90°,由等腰三角形的性质结合∠BCD=∠A,即可得出∠OCD=90°,即CD是⊙O的切线;
(2)在Rt△OCD中,由勾股定理可求出OD的值,进而可得出BD的长.
试题解析:(1)如图,连接OC.
∵AB是⊙O的直径,C是⊙O上一点,
∴∠ACB=90°,即∠ACO+∠OCB=90°.
∵OA=OC,∠BCD=∠A,
∴∠ACO=∠A=∠BCD,
∴∠BCD+∠OCB=90°,即∠OCD=90°,
∴CD是⊙O的切线.
(2)在Rt△OCD中,∠OCD=90°,OC=3,CD=4,
∴OD=![]() =5,
=5,
∴BD=OD﹣OB=5﹣3=2.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知A1(1,0),A2(1,1),A3(-1,1),A4(-1,-1),A5(2,-1),…,则A2017的坐标为( )
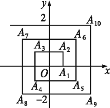
A.(505,504)B.(505,-504)C.(-504,504)D.(-504,-504)
-
科目: 来源: 题型:
查看答案和解析>>【题目】某产品的生产流水线每小时生产100件产品,生产前没有产品积压,生产3h后安排工人装箱,若每小时装产品150件,未装箱的产品数量y是时间t的函数,那么,这个函数的大致图象只能是下图中的( )
A.
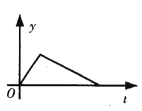 B.
B. 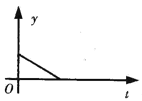
C.
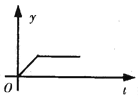 D.
D. 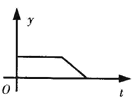
-
科目: 来源: 题型:
查看答案和解析>>【题目】
 ,
, 是平面直角坐标系中的任意两点,我们把
是平面直角坐标系中的任意两点,我们把 叫做P1,P2两点间的“直角距离”,记作d(P1,P2);比如:点P(2,-4),Q(1,0),则d(P,Q)=
叫做P1,P2两点间的“直角距离”,记作d(P1,P2);比如:点P(2,-4),Q(1,0),则d(P,Q)= ,已知Q(2,1),动点P(x,y)满足d(P,Q)=3,且x,y均为整数,则满足条件的点P有________个.
,已知Q(2,1),动点P(x,y)满足d(P,Q)=3,且x,y均为整数,则满足条件的点P有________个. -
科目: 来源: 题型:
查看答案和解析>>【题目】一次函数图像经过点(4,-1),且与直线
 平行,求一次函数解析式和这个函数图像与两坐标轴围成的三角形的面积.
平行,求一次函数解析式和这个函数图像与两坐标轴围成的三角形的面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】随着社会的发展,通过微信朋友圈发布自己每天行走的步数已经成为一种时尚.“健身达人”小陈为了了解他的好友的运动情况.随机抽取了部分好友进行调查,把他们6月1日那天行走的情况分为四个类别:A(0~5000步)(说明:“0~5000”表示大于等于0,小于等于5000,下同),B(5001~10000步),C(10001~15000步),D(15000步以上),统计结果如图所示:
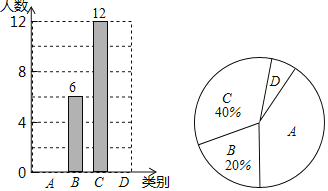
请依据统计结果回答下列问题:
(1)本次调查中,一共调查了 位好友.
(2)已知A类好友人数是D类好友人数的5倍.
①请补全条形图;
②扇形图中,“A”对应扇形的圆心角为 度.
③若小陈微信朋友圈共有好友150人,请根据调查数据估计大约有多少位好友6月1日这天行走的步数超过10000步?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,线段AB、CD分别是一辆轿车的邮箱剩余油量
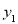 (升)与另一辆客车的油箱剩余油量
(升)与另一辆客车的油箱剩余油量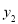 (升)关于行驶路程
(升)关于行驶路程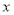 (千米)的函数图像.
(千米)的函数图像.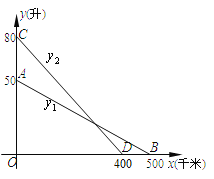
(1)分别求
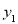 、
、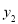 关于
关于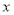 函数解析式,并写出定义域.
函数解析式,并写出定义域.(2)如果两车同时出发,轿车的行驶速度为每小时100千米,客车的行驶速度为每小时80千米,当邮箱的剩余油量相同,两车行驶的时间相差几分钟.
相关试题

