【题目】在△ABC中,∠A=120°,AB的垂直平分线交BC于M,交AB于E,AC的垂直平分线交BC于N,交AC于F,
(1) 如图(1),连接AM、AN,求∠MAN的度数。
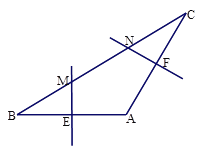
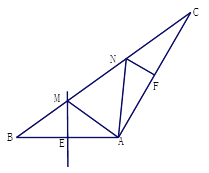
(2) 如图(2),如果AB=AC, 求证:BM=MN=NC.
参考答案:
【答案】(1)60 (2)见解析
【解析】试题分析:(1)由AB的垂直平分线交BC于M,交AB于E,AC的垂直平分线交BC于N,交AC于F,根据线段垂直平分线的性质,可得AM=BM,AN=CN,继而求得∠B=∠BAM=30°,∠C=∠CAN=30°,则可求得∠MAN的大小;
(2)由∠B=∠BAM=30°,∠C=∠CAN=30°,易证得△AMN是等边三角形,则可证得BM=MN=NC.
试题解析:
(1)∠MAN=60°.
理由:∵在△ABC中,AB=AC,∠BAC=120°,
∴∠B=∠C=30°,
∵ME是AB的垂直平分线,NF是AC的垂直平分线,
∴AM=BM,AN=CN,
∴∠B=∠BAM=30°,∠C=∠CAN=30°,
∴∠MAN=∠BAC-∠BAM-∠CAN=60°;
(2)证明:∵∠B=∠BAM=30°,∠C=∠CAN=30°,
∴∠AMN=∠ANM=60°,
∵∠MAN=60°,
∴△AMN是等边三角形,
∴AM=AN=MN,
∵AM=BM,AN=CN,
∴BM=MN=NC.
-
科目: 来源: 题型:
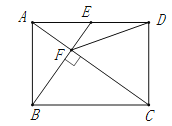
查看答案和解析>>【题目】如图,在矩形ABCD中,E是AD边的中点,BE⊥AC,垂足为点F,连接DF,分析下列四个结论:①△AEF∽△CAB;②CF=2AF;③DF=DC;④tan∠CAD=.其中正确的结论有( )
A.4个 B.3个 C.2个 D.1个
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图①,△ABC中,∠ABC、∠ACB的平分线交于O点,过O点作BC平行线交AB、AC于E、F.
探究一:请写出图①中线段EF与BE、CF间的关系,并说明理由.
探究二:如图②,△ABC若∠ABC的平分线与△ABC的外角平分线交于O,过点O作BC的平行线交AB于E,交AC于F.这时EF与BE、CF的关系又如何? 请直接写出关系式,不需要说明理由.


-
科目: 来源: 题型:
查看答案和解析>>【题目】下列各组数中,不相等的一组是( )
A. (﹣23)和﹣23 B. (﹣2)2和22 C. (﹣2)4和﹣24 D. |﹣23|和|2|3
-
科目: 来源: 题型:
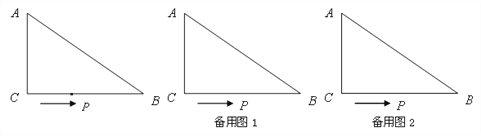
查看答案和解析>>【题目】如图,在△ABC中,∠ACB=90°,AC=6cm,BC=8cm,动点P从点C出发,按C→B→A的路径,以2cm每秒的速度运动,设运动时间为t秒.
(1) 当t=1时,求△ACP的面积
(2) t为何值时,线段AP是∠CAB的平分线?
(3) 请利用备用图2继续探索:当t为何值时,△ACP是以AC为腰的等腰三角形?
-
科目: 来源: 题型:
查看答案和解析>>【题目】某商场以每件120元的价格购进了某种品牌的衬衫600件,并以每件140元的价格销售了500件,由于天气原因,商场准备采取促销措施,问剩下的衬衫促销价格定为每件多少元时,销售完这批衬衫恰好盈利10800元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】若(x﹣3)2+|y+2|=0,则x+y=_____.
相关试题

