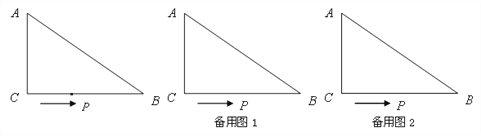
【题目】如图,在△ABC中,∠ACB=90°,AC=6cm,BC=8cm,动点P从点C出发,按C→B→A的路径,以2cm每秒的速度运动,设运动时间为t秒.
(1) 当t=1时,求△ACP的面积
(2) t为何值时,线段AP是∠CAB的平分线?
(3) 请利用备用图2继续探索:当t为何值时,△ACP是以AC为腰的等腰三角形?
参考答案:
【答案】(1).6;(2).1.5;(3)3,6或5.4
【解析】试题分析:(1)把t=1代入得出CP=2,利用三角形的面积进行解答即可;
(2)过P作PE⊥AB,设CP=2t,根据角平分线的性质和勾股定理进行解答即可;
(3)根据AC=CP,利用等腰直角三角形的性质解答即可.
试题解析:
(1)把t=1得出CP=2,所以△ACP的面积=![]() ×2×6=6cm2;
×2×6=6cm2;
(2)过P作PE⊥AB,如图1: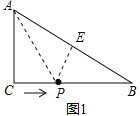
CP=2t,BP=(8-2t)cm,AE=AC=6cm,PE=CP=2t,BE=10-6=4,
可得:(8-2t)2=(2t)2-42
解得:t=![]() s;
s;
(3)如图2,3,4: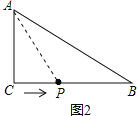
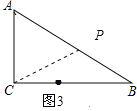
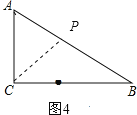
因为△ACP是以AC为腰的等腰三角形,
当AC=CP=6时,t1=6÷2=3s;
当AC=CP=6时,t2=4+![]() =
=![]() s;
s;
当AC=AP=6时,t3=4+2=6s.
所以当t为3,6, ![]() 时,△ACP是以AC为腰的等腰三角形.
时,△ACP是以AC为腰的等腰三角形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图①,△ABC中,∠ABC、∠ACB的平分线交于O点,过O点作BC平行线交AB、AC于E、F.
探究一:请写出图①中线段EF与BE、CF间的关系,并说明理由.
探究二:如图②,△ABC若∠ABC的平分线与△ABC的外角平分线交于O,过点O作BC的平行线交AB于E,交AC于F.这时EF与BE、CF的关系又如何? 请直接写出关系式,不需要说明理由.


-
科目: 来源: 题型:
查看答案和解析>>【题目】下列各组数中,不相等的一组是( )
A. (﹣23)和﹣23 B. (﹣2)2和22 C. (﹣2)4和﹣24 D. |﹣23|和|2|3
-
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC中,∠A=120°,AB的垂直平分线交BC于M,交AB于E,AC的垂直平分线交BC于N,交AC于F,
(1) 如图(1),连接AM、AN,求∠MAN的度数。
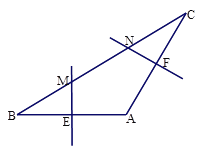
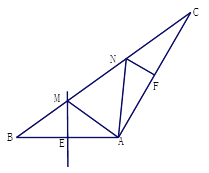
(2) 如图(2),如果AB=AC, 求证:BM=MN=NC.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某商场以每件120元的价格购进了某种品牌的衬衫600件,并以每件140元的价格销售了500件,由于天气原因,商场准备采取促销措施,问剩下的衬衫促销价格定为每件多少元时,销售完这批衬衫恰好盈利10800元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】若(x﹣3)2+|y+2|=0,则x+y=_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若□×3xy=3x2y,则□内应填的单项式是( )
A.xy
B.3xy
C.x
D.3x
相关试题

