【题目】如图,直线y= ![]() x+4与x轴、y轴分别交于点A和点B,点C、D分别为线段AB、OB的中点,点P为OA上一动点,PC+PD值最小时点P的坐标为( )
x+4与x轴、y轴分别交于点A和点B,点C、D分别为线段AB、OB的中点,点P为OA上一动点,PC+PD值最小时点P的坐标为( )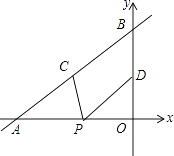
A.(﹣3,0)
B.(﹣6,0)
C.(﹣ ![]() ,0)
,0)
D.(﹣ ![]() ,0)
,0)
参考答案:
【答案】C
【解析】解:(方法一)作点D关于x轴的对称点D′,连接CD′交x轴于点P,此时PC+PD值最小,如图所示.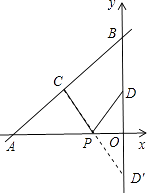
令y= ![]() x+4中x=0,则y=4,
x+4中x=0,则y=4,
∴点B的坐标为(0,4);
令y= ![]() x+4中y=0,则
x+4中y=0,则 ![]() x+4=0,解得:x=﹣6,
x+4=0,解得:x=﹣6,
∴点A的坐标为(﹣6,0).
∵点C、D分别为线段AB、OB的中点,
∴点C(﹣3,2),点D(0,2).
∵点D′和点D关于x轴对称,
∴点D′的坐标为(0,﹣2).
设直线CD′的解析式为y=kx+b,
∵直线CD′过点C(﹣3,2),D′(0,﹣2),
∴有 ![]() ,解得:
,解得: 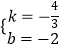 ,
,
∴直线CD′的解析式为y=﹣ ![]() x﹣2.
x﹣2.
令y=﹣ ![]() x﹣2中y=0,则0=﹣
x﹣2中y=0,则0=﹣ ![]() x﹣2,解得:x=﹣
x﹣2,解得:x=﹣ ![]() ,
,
∴点P的坐标为(﹣ ![]() ,0).
,0).
故选C.
(方法二)连接CD,作点D关于x轴的对称点D′,连接CD′交x轴于点P,此时PC+PD值最小,如图所示.
令y= ![]() x+4中x=0,则y=4,
x+4中x=0,则y=4,
∴点B的坐标为(0,4);
令y= ![]() x+4中y=0,则
x+4中y=0,则 ![]() x+4=0,解得:x=﹣6,
x+4=0,解得:x=﹣6,
∴点A的坐标为(﹣6,0).
∵点C、D分别为线段AB、OB的中点,
∴点C(﹣3,2),点D(0,2),CD∥x轴,
∵点D′和点D关于x轴对称,
∴点D′的坐标为(0,﹣2),点O为线段DD′的中点.
又∵OP∥CD,
∴点P为线段CD′的中点,
∴点P的坐标为(﹣ ![]() ,0).
,0).
故选C.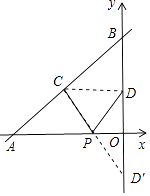
(方法一)根据一次函数解析式求出点A、B的坐标,再由中点坐标公式求出点C、D的坐标,根据对称的性质找出点D′的坐标,结合点C、D′的坐标求出直线CD′的解析式,令y=0即可求出x的值,从而得出点P的坐标.
(方法二)根据一次函数解析式求出点A、B的坐标,再由中点坐标公式求出点C、D的坐标,根据对称的性质找出点D′的坐标,根据三角形中位线定理即可得出点P为线段CD′的中点,由此即可得出点P的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】解方程:
(1)4x+3(2x﹣3)=12﹣(x﹣4)
(2)

(3)

-
科目: 来源: 题型:
查看答案和解析>>【题目】解答下列问题:
(1)一项工程,甲队单独做需10天完成,乙队单独做需15天完成,甲先做5天后,甲、乙合作完成余下的工作,问两队合做几天可以完成这项工作?
(2)从A地到B地,甲需走10小时,从B地到A地,乙需走15小时,甲、乙两人从A,B两地相向而行,甲出发5小时后乙出发,问乙出发几小时后两人相遇?
(3)一笔钱款,可以买甲种商品10件或买乙种商品15件,用这笔钱款买了甲、乙两种商品,已知甲种商品比乙种商品多买了5件,问乙种商品买了几件?
(4)通过解答上面三个问题,你发现了什么?
(5)根据上面所列的方程,编写一道实际问题的应用题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】我国是世界上严重缺水的国家之一.为了倡导“节约用水从我做起”,小刚在他所在班的50名同学中,随机调查了10名同学家庭中一年的月均用水量(单位:t),并将调查结果绘成了如下的条形统计图
【1】求这10个样本数据的平均数、众数和中位数;
【2】根据样本数据,估计小刚所在班50名同学家庭中月均用水量不超过7 t的约有多少户.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在ABCD中,AB为⊙O的直径,⊙O与DC相切于点E,与AD相交于点F,已知AB=12,∠C=60°,则
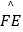 的长为 .
的长为 . 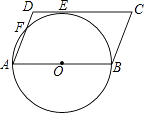
-
科目: 来源: 题型:
查看答案和解析>>【题目】在矩形ABCD中,∠B的角平分线BE与AD交于点E,∠BED的角平分线EF与DC交于点F,若AB=9,DF=2FC,则BC= . (结果保留根号)

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在ABCD中,AE⊥BC于点E,延长BC至点F使CF=BE,连结AF,DE,DF.
(1)求证:四边形AEFD是矩形;
(2)若AB=6,DE=8,BF=10,求AE的长.

相关试题

