【题目】如图,点C是以AB为直径的圆O上一点,直线AC与过B点的切线相交于D,点E是BD的中点,直线CE交直线AB于点F.
(1)求证:CF是⊙O的切线;
(2)若ED=3,EF=5,求⊙O的半径.
参考答案:
【答案】
(1)证明:连CB、OC,如图,

∵BD为⊙O的切线,
∴DB⊥AB,
∴∠ABD=90°,
∵AB是直径,
∴∠ACB=90°,
∴∠BCD=90°,
∵E为BD的中点,
∴CE=BE,
∴∠BCE=∠CBE,
而∠OCB=∠OBC,
∴∠OBC+∠CBE=∠OCB+∠BCE=90°,
∴OC⊥CF,
∴CF是⊙O的切线
(2)解:CE=BE=DE=3,
∵EF=5,
∴CF=CE+EF=8,
∵∠ABD=90°,
∴∠EBF=90°,
∵∠OCF=90°,
∴∠EBF=∠OCF,
∵∠F=∠F,
∴△EBF∽△OCF,
∴ ![]() ,
,
∴ ![]() ,
,
∴OC=6,
即⊙O的半径为6.
【解析】已知圆的直径,常添加辅助线是连接弦,构造圆周角是直角;要证某一直线是圆的切线,添加辅助线的方法是“连半径,证垂直”或“作垂线,证半径”。(1)连CB、OC根据直径所对的圆周角是直角,得出∠ABD=∠BCD=90°,在Rt△BCD中,因为点E是BD的中点,根据直角三角形斜边上的中线等于斜边的一半,得出EC=BE,得到E∠BCE=∠CBE,于是就可以证得∠OCE=90°,根据切线的判定定理就可以得到CF是⊙O的切线;(2)由(1)的证明过程可知CE=BE=DE=3,而EF=5,可以得到CF=8,易证△EBF∽△OCF,从而求得圆的半径长,。
【考点精析】本题主要考查了直角三角形斜边上的中线和相似三角形的判定与性质的相关知识点,需要掌握直角三角形斜边上的中线等于斜边的一半;相似三角形的一切对应线段(对应高、对应中线、对应角平分线、外接圆半径、内切圆半径等)的比等于相似比;相似三角形周长的比等于相似比;相似三角形面积的比等于相似比的平方才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图BD为△ABC的角平分线,且BD=BC, E为BD延长线上一点,BE=BA,
过E作EF⊥AB于F,下列结论:
①△ABD≌△EBC ;②∠BCE+∠BDC=180°;
③AD=AE=EC;④AB//CE ;
⑤BA+BC=2BF.其中正确的是________________.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,某校有一块长为(3a+b)m,宽为(2a+b)m的长方形空地,中间是边长(a+b)m的正方形草坪,其余为活动场地,学校计划将活动场地(阴影部分)进行硬化.
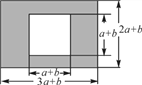
(1)用含a,b的代数式表示需要硬化的面积并化简;
(2)当a=5,b=2时,求需要硬化的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】成都市的水费实行下表的收费方式:
每月用水量
单价
不超出
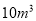 (包括
(包括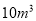 )
)2元/
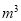
超出
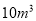 但不超出
但不超出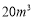 (包括
(包括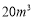 )的部分
)的部分3元/
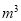
超出
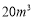 的部分
的部分4元/
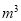
(1)周老师家九月份用了
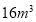 的水,应付多少水费?
的水,应付多少水费?(2)如果李老师家九月份的用水量为
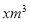 ,那么应付的水费为多少元?
,那么应付的水费为多少元?(3)如果曹老师家九月和十月一共用了
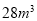 的水,且已知九月比十月少,设九月用水量为
的水,且已知九月比十月少,设九月用水量为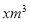 ,那么曹老师这两个月一共要交多少钱的水费?(可用含
,那么曹老师这两个月一共要交多少钱的水费?(可用含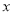 的代数式表示)
的代数式表示) -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在
 中,
中, ,
, ,
, 为
为 延长线上一点,点
延长线上一点,点 在
在 上,且
上,且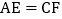 .
.(1)求证:
 ;
;(2)若
 ,求
,求 的度数.
的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】小明把一副三角板按如图所示叠放在一起,固定三角板
 ,将另一块三角板
,将另一块三角板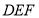 绕公共顶点
绕公共顶点 顺时针旋转(旋转的角度为锐角).若两块三角板有一边平行,则三角板
顺时针旋转(旋转的角度为锐角).若两块三角板有一边平行,则三角板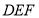 旋转的度数可能是______.
旋转的度数可能是______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在某体育用品商店,购买50根跳绳和80个毽子共用1120元,购买30根跳绳和50个毽子共用680元.
(1)跳绳、毽子的单价各是多少元?
(2)该店在“元旦”节期间开展促销活动,所有商品按同样的折数打折销售.节日期间购买100根跳绳和100个毽子只需1700元,该店的商品按原价的几折销售?
相关试题

