【题目】(12分)已知,在平面直角坐标系中,AB⊥x轴于点B,点A(a,b)满足![]() +|b-2|=0,平移线段AB使点A与原点重合,点B的对应点为点C.
+|b-2|=0,平移线段AB使点A与原点重合,点B的对应点为点C.
(1)则a=____,b=____;点C坐标为________;
(2)如下图所示:点D(m, n)在线段BC上,求m、n满足的关系式;

(3)如下图所示:E是线段OB上一动点,以OB为边作∠G=∠AOB,,交BC于点G,连CE交OG于点F,的当点E在线段OB上运动过程中, ![]() 的值是否会发生变化?若变化请说明理由,若不变,请求出其值.
的值是否会发生变化?若变化请说明理由,若不变,请求出其值.

参考答案:
【答案】 (1)4 2 (0,-2);(2)m-2n=4;(3)不变, ![]() 理由见解析.
理由见解析.
【解析】(1)a= 4 ;b= 2 ;点C的坐标为(0,-2).
(2)如图1,过点D分别作DM⊥x轴于点M, DN⊥y轴于点N,连接OD.
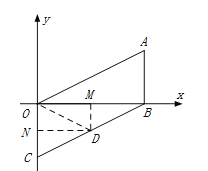
∵AB⊥ x轴于点B,且点A,D,C三点的坐标分别为:(4,2),(m,n),(0,-2)
∴OB=4,OC=2,MD=-n,ND=m
∴ S△BOC=![]()
![]() OB×OC=4
OB×OC=4
又∵S△BOC = S△BOD+S△COD
=![]() OB×MD+
OB×MD+![]() OC×ND
OC×ND
=![]() ×4×(-n)+
×4×(-n)+![]() ×m×2
×m×2
=m-2n
∴m-2n=4…………(7分)
(3)解: ![]()
![]() 的值不变,值为2.理由如下:
的值不变,值为2.理由如下:
如图所示:分别过点E,F作EP∥OA, FQ∥OA分别交y轴于点P,点Q

∵线段OC是由线段AB平移得到
∴BC∥OA 又∵EP∥OA
∴EP∥BC
∴∠GCF=∠PEC
∵EP∥OA
∴∠AOE=∠OEP
∴∠OEC=∠OEP+∠PEC
=∠AOE+∠GCF 同理:∠OFC=∠AOF+∠GCF…………(10分)
又∵∠AOB=∠BOG
∴∠OFC=2∠AOE+∠GCF
∴![]()
![]()
![]() =2
=2
-
科目: 来源: 题型:
查看答案和解析>>【题目】在直角三角形ABC中,已知∠C=90°,∠A=40°,BC=3,则AC=( )
A.3sin40°
B.3sin50°
C.3tan40°
D.3tan50° -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,A(1,1),B(-1,1),C(-1,-2),D(1,-2).把一条长为2018个单位长度且没有弹性的细线(线的粗细忽略不计)的一端固定在点A处,并按A-B-C-D…的规律绕在ABCD的边上,则细线另一端所在位置的点的坐标是( )
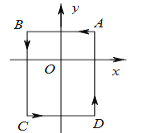
A. (-1,0)B. (1,2)C. (1,-1)D. (0,-2)
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,A、B、C三点的坐标分别为(﹣6,7)、(﹣3,0)、(0,3).
(1)画出△ABC,并求△ABC的面积;
(2)在△ABC中,点C经过平移后的对应点为C′(5,4),将△ABC作同样的平移得到△A′B′C′, 画出平移后的△A′B′C′,并写出点A′,B′的坐标;
(3)已知点P(﹣3,m)为△ABC内一点,将点P向右平移4个单位后,再向下平移6个单位得到点Q(n,﹣3),则m= ,n= .

-
科目: 来源: 题型:
查看答案和解析>>【题目】看图填空,并在括号内说明理由: 如图,已知∠BAP与∠APD互补,∠1=∠2,说明∠E=∠F.
证明:∵∠BAP与∠APD互补(_________), ∴AB∥CD(____________),
∴∠BAP=∠APC(__________).
又∵∠1=∠2(__________),
∴∠BAP﹣∠1=∠APC﹣∠2(_________),即∠3=∠4,
∴AE∥PF,(___________),
∴∠E=∠F(__________).

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,等腰△ABC的底边BC=20,面积为120,点F在边BC上,且BF=3FC,EG是腰AC的垂直平分线,若点D在EG上运动,则△CDF周长的最小值为__.

-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)已知2a-1的平方根是±3,3a-b+2的算术平方根是4,求a+3b的立方根.
(2)已知a,b ,c满足
 ,求a,b c的值。
,求a,b c的值。
相关试题

