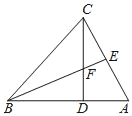
【题目】如图,在△CBD中,CD=BD,CD⊥BD,BE平分∠CBA交CD于点F,CE⊥BE垂足是E,CE与BD交于点A.求证:
(1)BF=AC;
(2)BE是AC的中垂线;
(3)若AD=2,求AB的长.
参考答案:
【答案】(1)见解析;(2)见解析;(3)4+2![]() .
.
【解析】
(1)由 CD⊥AB,BE⊥AC,可得BDF=∠ADC=∠AEB=90°,DBF=∠DCA,继而证明出△BDF≌△CDA可得结论;
(2) BE平分∠ABC,可证∠A=∠BCA,BC=BA ,CE=EA可得结论;
(3) 由(1)BDF≌△CDA,可得各边的长,可求出AB的长.
(1)证明:∵CD⊥AB,BE⊥AC,
∴∠BDF=∠ADC=∠AEB=90°,
∵∠DBF+∠A=90°,∠DCA+∠A=90°,
∴∠DBF=∠DCA,
∵BD=CD,
∴△BDF≌△CDA(SAS),
∴BF=AC.
(2)证明:∵BE平分∠ABC,
∴∠ABE=∠CBE,
∵∠BEA=∠BEC=90°,
∴∠A+∠ABE=90°,∠BCA+∠CBE=90°,
∴∠A=∠BCA,
∴BC=BA,
∵BE⊥AC,
∴CE=EA,
∴BE是AC的中垂线.
(3)解:连接AF.

∵△BDF≌△CDA,
∴AD=DF=2,AF=2![]() ,
,
∵BE垂直平分AC,
∴CF=AF=2![]() ,
,
∴BD=CD=2+2![]() ,
,
∴AB=BD+AD=4+2![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,P是BC上的点,作PQ∥AC交AB于点Q,分别作PR⊥AB,PS⊥AC,垂足分别是R,S,若PR=PS,则下面三个结论:①AS=AR;②AQ=PQ;③△PQR≌△CPS;④AC﹣AQ=2SC,其中正确的是( )
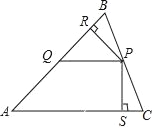
A. ②③④ B. ①② C. ①④ D. ①②③④
-
科目: 来源: 题型:
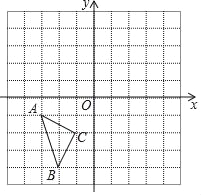
查看答案和解析>>【题目】在如图所示的直角坐标系中,每个小方格都是边长为1的正方形,△ABC的顶点均在格点上,点A的坐标是(﹣3,﹣1).
(1)将△ABC关于x轴对称得到△A1B1C1,画出△A1B1C1,并写出点B1的坐标;
(2)把△A1B1C1平移,使点B1平移到B2(3,4),请作出△A1B1C1平移后的△A2B2C2,并写出A2的坐标;
(3)已知△ABC中有一点D(a,b),求△A2B2C2中的对应点D2的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了抓住梵净山文化艺术节的商机,某商店决定购进A、B两种艺术节纪念品.若购进A种纪念品8件,B种纪念品3件,需要950元;若购进A种纪念品5件,B种纪念品6件,需要800元.
(1)求购进A、B两种纪念品每件各需多少元?
(2)若该商店决定购进这两种纪念品共100件,考虑市场需求和资金周转,用于购买这100件纪念品的资金不少于7500元,但不超过7650元,那么该商店共有几种进货方案?
(3)若销售每件A种纪念品可获利润20元,每件B种纪念品可获利润30元,在第(2)问的各种进货方案中,哪一种方案获利最大?最大利润是多少元?
-
科目: 来源: 题型:
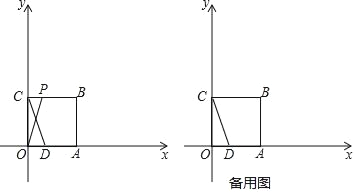
查看答案和解析>>【题目】如图,在平面直角坐标系中,O是坐标原点,正方形OABC的顶点A、C分别在x轴与y轴上,已知正方形边长为3,点D为x轴上一点,其坐标为(1,0),连接CD,点P从点C出发以每秒1个单位的速度沿折线C→B→A的方向向终点A运动,当点P与点A重合时停止运动,运动时间为t秒.
(1)连接OP,当点P在线段BC上运动,且满足△CPO≌△ODC时,求直线OP的表达式;
(2)连接PC,求△CPD的面积S关于t的函数表达式;
(3)点P在运动过程中,是否存在某个位置使得△CDP为等腰三角形,若存在,直接写出点P的坐标,若不存在,说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,∠AOB=30,∠AOB 内有一定点 P,且 OP=12,在 OA 上有一动点 Q,OB 上有 一动点 R。若△PQR 周长最小,则最小周长是( )
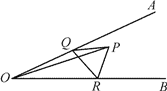
A. 6 B. 12 C. 16 D. 20
-
科目: 来源: 题型:
查看答案和解析>>【题目】把一边长为40cm的正方形硬纸板,进行适当的剪裁,折成一个长方形盒子(纸板的厚度忽略不计).
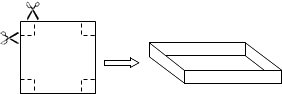
(1)如图,若在正方形硬纸板的四角各剪一个同样大小的正方形,将剩余部分折成一个无盖的长方形盒子. ①要使折成的长方形盒子的底面积为484cm2 , 那么剪掉的正方形的边长为多少?
②折成的长方形盒子的侧面积是否有最大值?如果有,求出这个最大值和此时剪掉的正方形的边长;如果没有,说明理由.
(2)若在正方形硬纸板的四周剪掉一些矩形(即剪掉的矩形至少有一条边在正方形硬纸板的边上),将剩余部分折成一个有盖的长方形盒子,若折成的一个长方形盒子的表面积为550cm2 , 求此时长方形盒子的长、宽、高(只需求出符合要求的一种情况).
相关试题

