【题目】在△ABC中,D是BC的中点,且AD=AC,DE⊥BC,与AB相交于点E,EC与AD相交于点F.

(1)求证:△ABC∽△FCD;
(2)若DE=3,BC=8,求△FCD的面积.
参考答案:
【答案】(1)证明见试题解析;(2)4.5.
【解析】
试题分析:(1)利用D是BC边上的中点,DE⊥BC可以得到∠EBC=∠ECB,而由AD=AC可以得到∠ADC=∠ACD,再利用相似三角形的判定,就可以证明题目结论;
(2)过点A作AM⊥BC,垂足是M,利用等腰三角形性质求出DM,利用平行线性质定理,求出AM,从而求出△ABC的面积,再利用相似三角形的性质就可以求出三角形FCD的面积.
试题解析:(1)∵D是BC边上的中点,DE⊥BC,∴BD=DC,∠EDB=∠EDC=90°,∴△BDE≌△EDC,∴∠B=∠DCE,∵AD=AC,∴∠ADC=∠ACB,∴△ABC∽△FCD;
(2)过点A作AM⊥BC,垂足是M,∵△ABC∽△FCD,BC=2CD,∴![]() ,
,![]() ,
,
∵DE⊥BC,∴D是BC边上的中点,∴BD=DC,∵BC=8,∴DC=4,∵AD=AC,AM⊥DC,∴DM=MC=2,∴BM=4+2=6,
∵DE⊥BC,AM⊥DC,∴DE∥AM,∴![]() ,∴
,∴![]() ,
,![]() ,,∴S△ABC=
,,∴S△ABC=![]() BC×AM=
BC×AM=![]() ,∵
,∵![]() ,∴
,∴![]() .
.

-
科目: 来源: 题型:
查看答案和解析>>【题目】一幢房屋的侧面外墙壁的形状如图所示,它由等腰三角形OCD和矩形ABCD组成,∠OCD=25°,外墙壁上用涂料涂成颜色相同的条纹,其中一块的形状是四边形EFGH,测得FG∥EH,GH=2.6m,∠FGB=65°.

(1)求证:GF⊥OC;
(2)求EF的长(结果精确到0.1m).
(参考数据:sin25°=cos65°≈0.42,cos25°=sin65°≈0.91)
-
科目: 来源: 题型:
查看答案和解析>>【题目】函数图象在探索函数的性质中有非常重要的作用,下面我们就一类特殊的函数展开探索,画函数
 的图象,经历分析解析式、列表、描点、连线过程得到函数图象如下图所示:
的图象,经历分析解析式、列表、描点、连线过程得到函数图象如下图所示:
……
-3
-2
-1
0
1
2
3
……

……
6
4
2
0
2
4
6
……
经历同样的过程画函数
 和
和 的图象如下图所示,观察发现:三个函数的图象都是由两条射线组成的轴对称图形:三个函数解析式中绝对值前面的系数相同,则图象的开口方向和形状完全相同,只有最高点和对称轴发生了变化.
的图象如下图所示,观察发现:三个函数的图象都是由两条射线组成的轴对称图形:三个函数解析式中绝对值前面的系数相同,则图象的开口方向和形状完全相同,只有最高点和对称轴发生了变化. 请直接写出
请直接写出 与
与 的交点坐标和函数
的交点坐标和函数 的对称轴;
的对称轴; 在所给的平面直角坐标系内画出函数
在所给的平面直角坐标系内画出函数 的图象(不列表),并写出函数
的图象(不列表),并写出函数 的一条性质;
的一条性质; 结合函数图像,直接写出不等式
结合函数图像,直接写出不等式 时
时 的取值范围.
的取值范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知
 是线段
是线段 上任意一点(端点除外),分别以
上任意一点(端点除外),分别以 为边,并且在
为边,并且在 的同一侧作等边
的同一侧作等边 和等边
和等边 ,连结
,连结 交
交 于
于 ,连结
,连结 交
交 于
于 ,给出以下三个结论:
,给出以下三个结论:
①
 ②
② ③
③ ,其中结论正确的个数是( )
,其中结论正确的个数是( )A.0B.1C.2D.3
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
 ,给出下列结论:①
,给出下列结论:① ②
② ③
③ ④
④ ,其中正确结论的序号______.
,其中正确结论的序号______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将Rt△ABC沿某条直线折叠,使斜边的两个端点A与B重合,折痕为DE.

(1)如果AC=6cm,BC=8cm,试求△ACD的周长;
(2)如果∠CAD:∠BAD=1:2,求∠B的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC内接于⊙O,BD为⊙O的直径,BD与AC相交于点H,AC的延长线与过点B的直线相交于点E,且∠A=∠EBC.
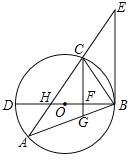
(1)求证:BE是⊙O的切线;
(2)已知CG∥EB,且CG与BD、BA分别相交于点F、G,若BGBA=48,FG=
 ,DF=2BF,求AH的值.
,DF=2BF,求AH的值.
相关试题

