【题目】函数图象在探索函数的性质中有非常重要的作用,下面我们就一类特殊的函数展开探索,画函数![]() 的图象,经历分析解析式、列表、描点、连线过程得到函数图象如下图所示:
的图象,经历分析解析式、列表、描点、连线过程得到函数图象如下图所示:
| …… | -3 | -2 | -1 | 0 | 1 | 2 | 3 | …… |
| …… | 6 | 4 | 2 | 0 | 2 | 4 | 6 | …… |
经历同样的过程画函数![]() 和
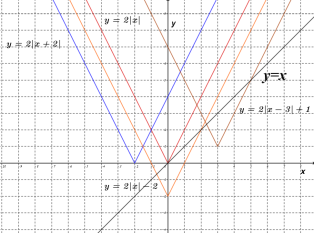
和![]() 的图象如下图所示,观察发现:三个函数的图象都是由两条射线组成的轴对称图形:三个函数解析式中绝对值前面的系数相同,则图象的开口方向和形状完全相同,只有最高点和对称轴发生了变化.
的图象如下图所示,观察发现:三个函数的图象都是由两条射线组成的轴对称图形:三个函数解析式中绝对值前面的系数相同,则图象的开口方向和形状完全相同,只有最高点和对称轴发生了变化.
![]() 请直接写出
请直接写出![]() 与
与![]() 的交点坐标和函数
的交点坐标和函数![]() 的对称轴;
的对称轴;
![]() 在所给的平面直角坐标系内画出函数
在所给的平面直角坐标系内画出函数![]() 的图象(不列表),并写出函数
的图象(不列表),并写出函数![]() 的一条性质;
的一条性质;
![]() 结合函数图像,直接写出不等式
结合函数图像,直接写出不等式![]() 时
时![]() 的取值范围.
的取值范围.

参考答案:
【答案】(1)交点坐标为(﹣1,2),对称轴为直线x=﹣2;(2)图像见解析,性质:函数![]() 的图象的对称轴为直线x=3(答案不唯一);(3)
的图象的对称轴为直线x=3(答案不唯一);(3)![]()
【解析】
(1)根据所给图像即可得到答案;
(2)画出函数![]() 的图象,结合所画图像即可得到相应的图像性质;
的图象,结合所画图像即可得到相应的图像性质;
(3)先画出![]() 的函数图像,再通过与
的函数图像,再通过与![]() 联立方程求出交点坐标,结合函数图像即可得到答案.
联立方程求出交点坐标,结合函数图像即可得到答案.
解:(1)由图像可知:![]() 与
与![]() 的交点坐标为(﹣1,2),
的交点坐标为(﹣1,2),
函数![]() 的对称轴为直线x=﹣2;
的对称轴为直线x=﹣2;
(2)函数![]() 的图象如图所示:
的图象如图所示:

性质:函数![]() 的图象的对称轴为直线x=3(答案不唯一);
的图象的对称轴为直线x=3(答案不唯一);
(3)函数![]() 的图像如图所示:
的图像如图所示:
令![]() ,
,
当![]() 时,
时,![]() ,
,
解得![]() ,
,
则![]() ,
,
∴![]() 与
与![]() 的一个交点坐标为(5,5),
的一个交点坐标为(5,5),
当![]() 时,
时,![]() ,
,
解得![]() ,
,
则![]() ,
,
∴![]() 与
与![]() 的另一个交点坐标为(
的另一个交点坐标为(![]() ,
,![]() ),
),
∴由图像可知:不等式![]() 的解集为
的解集为![]() ,
,
故答案为:![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如果
 的乘积不含
的乘积不含 和
和 项,那么
项,那么 和
和 值分别是( )
值分别是( )A.
 B.
B.
C.
 D.
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】重庆市有
 五个景区很受游客喜爱,一旅行社对某小区居民在暑假期间去以上五个景区旅游(只选一个景区)的意向做了一次随机调查统计,并根据这个统计结果制作了如下两幅不完整的统计图.
五个景区很受游客喜爱,一旅行社对某小区居民在暑假期间去以上五个景区旅游(只选一个景区)的意向做了一次随机调查统计,并根据这个统计结果制作了如下两幅不完整的统计图.
 该小区居民在这次随机调查中被调查到的人数是_______人,
该小区居民在这次随机调查中被调查到的人数是_______人,  想去
想去 景区的人有_________人, 并补全条形统计图.
景区的人有_________人, 并补全条形统计图. 被调查到的居民想去 景区旅游的人数最多,若该小区有居民
被调查到的居民想去 景区旅游的人数最多,若该小区有居民 人,估计去该景区旅游的居民约有多少人?
人,估计去该景区旅游的居民约有多少人? 小强同学赞假期间计划与父母从
小强同学赞假期间计划与父母从 五个景区中,任选两个去旅游,求选至
五个景区中,任选两个去旅游,求选至 两个景区的概率,(要求列表求概率)
两个景区的概率,(要求列表求概率) -
科目: 来源: 题型:
查看答案和解析>>【题目】一幢房屋的侧面外墙壁的形状如图所示,它由等腰三角形OCD和矩形ABCD组成,∠OCD=25°,外墙壁上用涂料涂成颜色相同的条纹,其中一块的形状是四边形EFGH,测得FG∥EH,GH=2.6m,∠FGB=65°.

(1)求证:GF⊥OC;
(2)求EF的长(结果精确到0.1m).
(参考数据:sin25°=cos65°≈0.42,cos25°=sin65°≈0.91)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知
 是线段
是线段 上任意一点(端点除外),分别以
上任意一点(端点除外),分别以 为边,并且在
为边,并且在 的同一侧作等边
的同一侧作等边 和等边
和等边 ,连结
,连结 交
交 于
于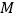 ,连结
,连结 交
交 于
于 ,给出以下三个结论:
,给出以下三个结论:
①
 ②
② ③
③ ,其中结论正确的个数是( )
,其中结论正确的个数是( )A.0B.1C.2D.3
-
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC中,D是BC的中点,且AD=AC,DE⊥BC,与AB相交于点E,EC与AD相交于点F.

(1)求证:△ABC∽△FCD;
(2)若DE=3,BC=8,求△FCD的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
 ,给出下列结论:①
,给出下列结论:① ②
② ③
③ ④
④ ,其中正确结论的序号______.
,其中正确结论的序号______.
相关试题

