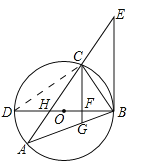
【题目】如图,△ABC内接于⊙O,BD为⊙O的直径,BD与AC相交于点H,AC的延长线与过点B的直线相交于点E,且∠A=∠EBC.
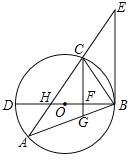
(1)求证:BE是⊙O的切线;
(2)已知CG∥EB,且CG与BD、BA分别相交于点F、G,若BGBA=48,FG=![]() ,DF=2BF,求AH的值.
,DF=2BF,求AH的值.
参考答案:
【答案】(1)证明见解析;(2)![]() .
.
【解析】
试题分析:(1)欲证明BE是⊙O的切线,只要证明∠EBD=90°.
(2)由△ABC∽△CBG,得![]() 求出BC,再由△BFC∽△BCD,得
求出BC,再由△BFC∽△BCD,得![]() =BFBD求出BF,CF,CG,GB,再通过计算发现CG=AG,进而可以证明CH=CB,求出AC即可解决问题.
=BFBD求出BF,CF,CG,GB,再通过计算发现CG=AG,进而可以证明CH=CB,求出AC即可解决问题.
试题解析:(1)连接CD,∵BD是直径,∴∠BCD=90°,即∠D+∠CBD=90°,∵∠A=∠D,∠A=∠EBC,∴∠CBD+∠EBC=90°,∴BE⊥BD,∴BE是⊙O切线.
(2)∵CG∥EB,∴∠BCG=∠EBC,∴∠A=∠BCG,∵∠CBG=∠ABC
∴△ABC∽△CBG,∴![]() ,即
,即![]() =BGBA=48,∴BC=
=BGBA=48,∴BC=![]() ,∵CG∥EB,∴CF⊥BD,∴△BFC∽△BCD,∴
,∵CG∥EB,∴CF⊥BD,∴△BFC∽△BCD,∴![]() =BFBD,∵DF=2BF,∴BF=4,在RT△BCF中,CF=
=BFBD,∵DF=2BF,∴BF=4,在RT△BCF中,CF=![]() =
=![]() ,∴CG=CF+FG=
,∴CG=CF+FG=![]() ,在RT△BFG中,BG=
,在RT△BFG中,BG=![]() =
=![]() ,∵BGBA=48,∴BA=
,∵BGBA=48,∴BA=![]() ,即AG=
,即AG=![]() ,∴CG=AG,∴∠A=∠ACG=∠BCG,∠CFH=∠CFB=90°,∴∠CHF=∠CBF,∴CH=CB=
,∴CG=AG,∴∠A=∠ACG=∠BCG,∠CFH=∠CFB=90°,∴∠CHF=∠CBF,∴CH=CB=![]() ,∵△ABC∽△CBG,∴
,∵△ABC∽△CBG,∴![]() ,∴AC=
,∴AC=![]() =
=![]() ,∴AH=AC﹣CH=
,∴AH=AC﹣CH=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】按要求取近似值,6209500≈___________(精确到万位,并用科学记数法表示)
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了解一批节能灯的使用寿命,宜采用__________的方式进行调查.(填“普查”或“抽样调查”)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,点O为坐标原点,直线l与抛物线
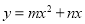 相交于A(1,
相交于A(1,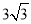 ),B(4,0)两点.
),B(4,0)两点.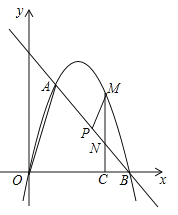
(1)求出抛物线的解析式;
(2)在坐标轴上是否存在点D,使得△ABD是以线段AB为斜边的直角三角形?若存在,求出点D的坐标;若不存在,说明理由;
(3)点P是线段AB上一动点,(点P不与点A、B重合),过点P作PM∥OA,交第一象限内的抛物线于点M,过点M作MC⊥x轴于点C,交AB于点N,若△BCN、△PMN的面积S△BCN、S△PMN满足S△BCN=2S△PMN,求出
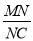 的值,并求出此时点M的坐标.
的值,并求出此时点M的坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】某中学举行“感恩资助,立志成才”演讲比赛,根据初赛成绩在七,八年级分别选出10名同学参加决赛,这些选手的决赛成绩如图所示:
根据图和下表提供的信息,解答下列问题:
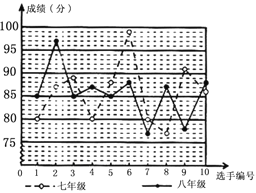
(1)请你把下边的表格填写完整;
成绩统计
众数
平均数
方差
七年级
85.7
39.61
八年级
85.7
27.81
(2)考虑平均数与方差,你认为哪年级的团体成绩更好些;
(3)假设在每个年级的决赛选手中分别选出3人参加总决赛,你认为哪个年级的实力更强一些,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列各式中,计算结果是x2+7x﹣18的是( )
A.(x﹣1)(x+18)
B.(x+2)(x+9)
C.(x﹣3)(x+6)
D.(x﹣2)(x+9) -
科目: 来源: 题型:
查看答案和解析>>【题目】在大量重复试验中,关于随机事件发生的频率与概率,下列说法正确的是( )
A.频率就是概率
B.频率与试验次数无关
C.概率是随机的,与频率无关
D.随着试验次数的增加,频率一般会越来越接近概率
相关试题

