【题目】如图,已知直线y1=﹣![]() x+1与x轴交于点A,与直线y2=﹣
x+1与x轴交于点A,与直线y2=﹣![]() x交于点B.
x交于点B.
(1)求△AOB的面积;
(2)求y1>y2时x的取值范围.

参考答案:
【答案】(1)1.5;(2)y1>y2时x>﹣1.
【解析】分析:(1)根据直线y1与x轴交于点A,令y=0时,求出x的值,得到点A的坐标,继而得到AO的长,再根据直线y1与直线y2交于点B,联立两个函数表达式求出B点的坐标,即可得到点B到OA的距离,利用三角形的面积公式求出![]() 的面积;
的面积;
(2)由(1)可知交点B的坐标是![]() ,根据图象在上的函数值大,由函数图象即可确定
,根据图象在上的函数值大,由函数图象即可确定![]() 时
时![]() 的取值范围.
的取值范围.
详解:(1)由![]() 可知,
可知,
当y=0时,x=2,
∴点A的坐标为(2,0),
∴![]()
∵直线![]() 与直线
与直线![]() 交于点B,
交于点B,
∴B点的坐标是![]() ,
,
∴![]() 的面积
的面积![]()
(2)由(1)可知交点B的坐标是![]() ,
,
由函数图象可知![]() 时,
时,![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】古希腊著名的毕达哥拉斯学派把1,3,6,10…这样的数称为“三角形数”,而把1,4,9,16…这样的数称为“正方形数”.从图中可以发现,任何一个大于1的“正方形数”都可以看作两个相邻“三角形数”之和.下列等式中,符合这一规律的是( )

A. 13=3+10 B. 25=9+16 C. 36=15+21 D. 49=18+31
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图是一个被抹去x轴、y轴及原点O的网格图,网格中每个小正方形的边长均为1个单位长度,三角形ABC的各顶点都在网格的格点上,若记点A的坐标为(﹣1,3),点C的坐标为(1,﹣1).
(1)请在图中找出x轴、y轴及原点O的位置;
(2)把△ABC向下平移2个单位长度,再向右平移3个单位长度,请你画出平移后的△A1B1C1,若△ABC内部一点P的坐标为(a,b),则点P的对应点P1的坐标是 ;
(3)试求出△ABC的面积.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知如图,⊙O的直径AB与弦AC的夹角∠A=30°,AC=CP.
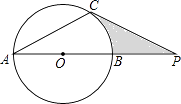
(1)求证:CP是⊙O的切线;
(2)若AB=4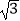 ,求图中阴影部分的面积.
,求图中阴影部分的面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】如下图是用棋子摆成的“T”字图案.从图案中可以看出,第一个“T”字图案需要5枚棋子,第二个“T”字图案需要8枚棋子,第三个“T”字图案需要11枚棋子

(1)照此规律,摆成第八个图案需要几枚棋子?
(2)摆成第n个图案需要几枚棋子?
(3)摆成第2008个图案需要几枚棋子?
-
科目: 来源: 题型:
查看答案和解析>>【题目】a、b、c在数轴上的位置如图所示,则:
(1)用“<、>、=”填空:a____0,b____0,c_____0;
(2)用“<、>、=”填空:﹣a____0,a﹣b____0,c﹣a____0;
(3)化简:|﹣a|﹣|a﹣b|+|c﹣a|

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示的运算程序中,若开始输入的x值为48,我们发现第一次输出的结果为24,第二次输出的结果为12,…,则第2018次输出的结果为________.
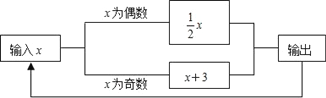
相关试题

