Question

【题目】如图，小明家在学校O的北偏东60°方向，距离学校80米的A处，小华家在学校O的南偏东45°方向的B处，小华家在小明家的正南方向，求小华家到学校的距离．（结果精确到1米，参考数据： ≈1.41， ≈1.73， ≈2.45）

Answer 1

【答案】解：由题意可知：作OC⊥AB于C，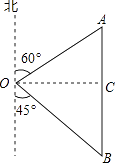

∠ACO=∠BCO=90°，∠AOC=30°，∠BOC=45°．
在Rt△ACO中，
∵∠ACO=90°，∠AOC=30°，
∴AC= AO=40m，OC= AC=40 m．
在Rt△BOC中，
∵∠BCO=90°，∠BOC=45°，
∴BC=OC=40 m．
∴OB= =40 ≈40×2.45≈82（米）．
答：小华家到学校的距离大约为82米．
【解析】作OC⊥AB于C，由已知可得△ABO中∠A=60°，∠B=45°且OA=80m，要求OB的长，可以先求出OC和BC的长．
【考点精析】根据题目的已知条件，利用关于方向角问题的相关知识可以得到问题的答案，需要掌握指北或指南方向线与目标方向 线所成的小于90°的水平角，叫做方向角．