Question

【题目】如图，PA是⊙O的切线，A为切点，AC是⊙O的直径，AB是弦，PA∥BC交AB于点D.

（1）求证：PB是⊙O的切线．
（2）当BC=2 ，cos∠AOD= 时，求PB的长．

Answer 1

【答案】
（1）证明：∵PA为⊙O的切线，

∴∠PAO=90°，

∵AC是⊙O的直径，

∴∠ABC=90°，

∵PO∥BC，

∴∠ADO=∠ABC=90°，即PO⊥AB，

∴AD=BD，

∴PA=PB，

在△APO和△BPO中，

，

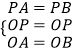∴△APO≌△BPO（SSS），

∴∠PAO=∠PBO=90°，

∴∠PBO=90°，

∴PB是⊙O的切线．

（2）∵PO∥BC，

∴∠ACB=∠AOD，

∴cos∠ACB=cos∠AOD= ，

∴ = ，

∴AC=2 ÷ =8，

∴OA= AC=4，

∵cos∠AOP= = ，

∴OP=8 ，

∴AP= =4 ，

∵PA=PB，

∴PB=4 ．

【解析】（1）证PB是⊙O的切线，需要证∠PBO=90°，可利用SSS证明△APO≌△BPO得出∠PAO=∠PBO；
（2）利用平行线的性质和已知可得cos∠ACB=cos∠AOD，利用三角函数的定义可求得AC的长，在Rt△AOP中利用三角函数可求出OP的长，在Rt△AOP中利用勾股定理求得AP，由切线长定理可得PB的长.
【考点精析】通过灵活运用解直角三角形，掌握解直角三角形的依据：①边的关系a2+b2=c2；②角的关系：A+B=90°；③边角关系：三角函数的定义．(注意：尽量避免使用中间数据和除法)即可以解答此题．