【题目】如图,在平面直角坐标系中,已知点B的坐标是(﹣1,0),并且OA=OC=4OB,动点P在过A,B,C三点的抛物线上.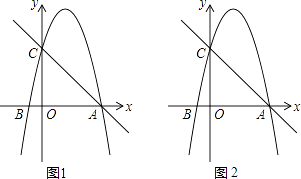
(1)求抛物线的解析式;
(2)是否存在点P,使得△ACP是以AC为直角边的直角三角形?若存在,求出所有符合条件的点P的坐标;若不存在,说明理由;
(3)过动点P作PE垂直于y轴于点E,交直线AC于点D,过点D作x轴的垂线.垂足为F,连接EF,当线段EF的长度最短时,写出点P的坐标(不要求写解题过程).
参考答案:
【答案】
(1)
解:由B(﹣1,0)可知OB=1,
∵OA=OC=4OB,
∴OA=OC=4,OB=1,
∴C(0,4),A(4,0).
设抛物线的解析式是y=ax2+bx+c,
则  ,
,
解得:  ,
,
则抛物线的解析式是y=﹣x2+3x+4;
(2)
解:存在.
①当以C为直角顶点时,
过点C作CP1⊥AC,交抛物线于点P1,
过点P1作y轴的垂线,垂足是M,M,如图1.
∵∠A CP1=90°,∴∠MCP1+∠ACO=90°.
∵∠ACO+∠OAC=90°,
∴∠MCP1=∠OAC.
∵OA=OC,
∴∠MCP1=∠OAC=45°,
∴∠MCP1=∠MP1C,
∴MC=MP1,
设P(m,﹣m2+3m+4),
则m=﹣m2+3m+4﹣4,
解得:m1=0(舍去),m2=2.
∴m=2,
此时﹣m2+3m+4=6,
∴P1P的坐标是(2,6).
②当点A为直角顶点时,
过A作AP2⊥AC交抛物线于点P2,
过点P2作y轴的垂线,垂足是N,AP交y轴于点F,如图2.
∴P2N∥x轴,
由∠CAO=45°得∠OAP2 =45°,
∴∠FP2N=45°,AO=OF.
∴P2N=NF,
设P2(n,﹣n2+3n+4),
则﹣n+4=﹣(﹣n2+3n+4),
解得:n1=﹣2,n2=4(舍去),
∴n=﹣2,
此时﹣n2+3n+4=﹣6,
∴P2的坐标是(﹣2,﹣6).
综上所述:P的坐标是(2,6)或(﹣2,﹣6);


(3)
解:当EF最短时,点P的坐标是( ![]() ,2)或(
,2)或( ![]() ,2).
,2).
解题过程如下:
连接OD,由题意可知,四边形OFDE是矩形,则OD=EF.
根据垂线段最短可得:当OD⊥AC时,OD(即EF)最短.
由(1)可知,在直角△AOC中,OC=OA=4.
根据等腰三角形的性质可得:D是AC的中点.
又∵DF∥OC,
∴△AFD∽△AOC,
∴ ![]() =
= ![]() =
= ![]()
∴DF= ![]() OC=2,
OC=2,
∴点D的纵坐标是2,
∴点P的纵坐标也是2,
解﹣x2+3x+4=2得,
x1= ![]() ,x2=
,x2= ![]() ,
,
∴点P的坐标为( ![]() ,2)或(
,2)或( ![]() ,2).
,2).
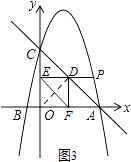
【解析】(1)只需求出A、B、C三点的坐标,然后运用待定系数法就可求出抛物线的解析式;(2)可分两种情况(①以C为直角顶点,②以A为直角顶点)讨论,然后根据点P的纵、横坐标之间的关系建立等量关系,就可求出点P的坐标;(3)连接OD , 易得四边形OFDE是矩形,则OD=EF , 根据垂线段最短可得当OD⊥AC时,OD(即EF)最短,然后只需求出点D的纵坐标,就可得到点P的纵坐标,就可求出点P的坐标.
【考点精析】本题主要考查了抛物线与坐标轴的交点的相关知识点,需要掌握一元二次方程的解是其对应的二次函数的图像与x轴的交点坐标.因此一元二次方程中的b2-4ac,在二次函数中表示图像与x轴是否有交点.当b2-4ac>0时,图像与x轴有两个交点;当b2-4ac=0时,图像与x轴有一个交点;当b2-4ac<0时,图像与x轴没有交点.才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在弹性限度内,弹簧挂上物体后会伸长,测得一弹簧的长度y(cm)与所挂物体的质量x(kg)之间的关系如下表,下列说法不正确的是( )
x/kg
0
1
2
3
4
5
y/cm
20
20.5
21
21.5
22
22.5
A. x与y都是变量,且x是自变量,y是x的函数
B. 弹簧不挂重物时的长度为0 cm
C. 物体质量每增加1 kg,弹簧长度y增加0.5 cm
D. 所挂物体质量为7 kg时,弹簧长度为23.5 cm
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,O为原点,点A(﹣2,0),点B(0,2),点E,点F分别为OA,OB的中点.若正方形OEDF绕点O顺时针旋转,得正方形OE′D′F′,记旋转角为α.

(1)如图①,当α=90°时,求AE′,BF′的长;
(2)如图②,当α=135°时,求证AE′=BF′,且AE′⊥BF′; -
科目: 来源: 题型:
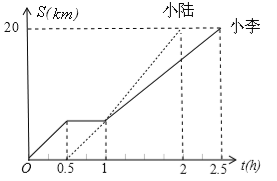
查看答案和解析>>【题目】小李和小陆从A地出发,骑自行车沿同一条路行驶到B地,他们离出发地的距离S(单位:km)和行驶时间t(单位:h)之间的函数关系的图象如图所示,根据图中的信息,有下列说法:
(1)他们都行驶了20 km;
(2)小陆全程共用了1.5h;
(3)小李和小陆相遇后,小李的速度小于小陆的速度
(4)小李在途中停留了0.5h。
其中正确的有
A.4个 B.3个 C.2个 D.1个
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,给下以下结论:
①2a﹣b=0;
②abc>0;
③4ac﹣b2<0;
④9a+3b+c<0;
⑤关于x的一元二次方程ax2+bx+c+3=0有两个相等实数根;
⑥8a+c<0.
其中正确的个数是( )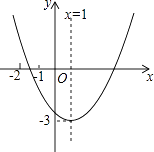
A.2
B.3
C.4
D.5 -
科目: 来源: 题型:
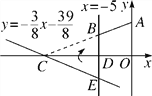
查看答案和解析>>【题目】如图,在平面直角坐标系xOy中,A(0,5),直线x=-5与x轴交于点D,直线y=-
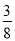 x-
x-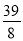 与x轴及直线x=-5分别交于点C,E.点B,E关于x轴对称,连接AB.
与x轴及直线x=-5分别交于点C,E.点B,E关于x轴对称,连接AB.(1)求点C,E的坐标及直线AB的解析式;
(2)若S=S△CDE+S四边形ABDO,求S的值;
(3)在求(2)中S时,嘉琪有个想法:“将△CDE沿x轴翻折到△CDB的位置,而△CDB与四边形ABDO拼接后可看成△AOC,这样求S便转化为直接求△AOC的面积,如此不更快捷吗?”但大家经反复验算,发现S△AOC≠S,请通过计算解释他的想法错在哪里.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知函数
 的图象与x轴、y轴分别交于点A,B,与函数y=x的图象交于点M,点M的横坐标为2.在x轴上有一点P (a,0)(其中a>2),过点P作x轴的垂线,分别交函数
的图象与x轴、y轴分别交于点A,B,与函数y=x的图象交于点M,点M的横坐标为2.在x轴上有一点P (a,0)(其中a>2),过点P作x轴的垂线,分别交函数 和y=x的图象于点C,D.
和y=x的图象于点C,D.(1)求点A的坐标;
(2)若OB=CD,求a的值.

相关试题

